题目内容
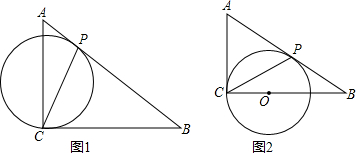
如图1,在Rt△ACB中,∠ACB=90°,AC=3,BC=4,有一过点C的动圆⊙O与斜边AB相切于动点P,连接CP.
(1)当⊙O与直角边AC相切时,如图2所示,求此时⊙O的半径r的长;
(2)随着切点P的位置不同,弦CP的长也会发生变化,试求出弦CP的长的取值范围.
(3)当切点P在何处时,⊙O的半径r有最大值?试求出这个最大值.
(1)当⊙O与直角边AC相切时,如图2所示,求此时⊙O的半径r的长;
(2)随着切点P的位置不同,弦CP的长也会发生变化,试求出弦CP的长的取值范围.
(3)当切点P在何处时,⊙O的半径r有最大值?试求出这个最大值.

考点:圆的综合题
专题:
分析:(1)先根据勾股定理求出AB的长,再由切线的性质求出PB的长,过P作PQ⊥BC于Q,过O作OR⊥PC于R,根据PQ∥AC得出PC的长,再由△COR∽△CPQ即可得出r的值;
(2)根据最短PC为AB边上的高,最大PC=BC=4即可得出结论;
(3)当P与B重合时,圆最大.这时,O在BD的垂直平分线上,过O作OD⊥BC于D,由BD=
BC=2,由于AB是切线可知∠ABO=90°,∠ABD+∠OBD=∠BOD+∠OBD=90°,故可得出∠ABC=∠BOD,根据锐角三角函数的定义即可得出结论.
(2)根据最短PC为AB边上的高,最大PC=BC=4即可得出结论;
(3)当P与B重合时,圆最大.这时,O在BD的垂直平分线上,过O作OD⊥BC于D,由BD=
| 1 |
| 2 |
解答: (1)解:如图1,∵在Rt△ACB中,∠ACB=90°,AC=3,BC=4,
(1)解:如图1,∵在Rt△ACB中,∠ACB=90°,AC=3,BC=4,
∴AB=
=
=5.
∵AC、AP都是圆的,圆心在BC上,AP=AC=3,
∴PB=2,
过P作PQ⊥BC于Q,过O作OR⊥PC于R,
∵PQ∥AC,
∴
=
=
=
,
∴PQ=
,BQ=
,
∴CQ=BC-BQ=
,
∴PC=
=
,
∵点O是CE的中点,
∴CR=
PC=
,
∴∠PCE=∠PCE,∠CRO=∠CQP,
∴△COR∽△CPQ,
∴
=
,即
=
,解得r=
;
(2)解:∵最短PC为AB边上的高,即PC=
=
,最大PC=BC=4,
∴
≤PC≤4;

(3)解:如图2,当P与B重合时,圆最大.O在BD的垂直平分线上,过O作OD⊥BC于D,由BD=
BC=2,
∵AB是切线,
∴∠ABO=90°,
∴∠ABD+∠OBD=∠BOD+∠OBD=90°,
∴∠ABC=∠BOD,
∴
=sin∠BOD=sin∠ABC=
=
,
∴OB=
,即半径最大值为
.
 (1)解:如图1,∵在Rt△ACB中,∠ACB=90°,AC=3,BC=4,
(1)解:如图1,∵在Rt△ACB中,∠ACB=90°,AC=3,BC=4,∴AB=
| AC2+BC2 |
| 32+42 |
∵AC、AP都是圆的,圆心在BC上,AP=AC=3,
∴PB=2,
过P作PQ⊥BC于Q,过O作OR⊥PC于R,
∵PQ∥AC,
∴
| PQ |
| PB |
| BQ |
| BC |
| AC |
| AB |
| 3 |
| 5 |
∴PQ=
| 6 |
| 5 |
| 8 |
| 5 |
∴CQ=BC-BQ=
| 12 |
| 5 |
∴PC=
| PQ2+CQ2 |
6
| ||
| 5 |
∵点O是CE的中点,
∴CR=
| 1 |
| 2 |
3
| ||
| 5 |
∴∠PCE=∠PCE,∠CRO=∠CQP,
∴△COR∽△CPQ,
∴
| OC |
| CR |
| PC |
| CQ |
| r | ||||
|
| ||||
|
| 3 |
| 2 |
(2)解:∵最短PC为AB边上的高,即PC=
| 3×4 |
| 5 |
| 12 |
| 5 |
∴
| 12 |
| 5 |

(3)解:如图2,当P与B重合时,圆最大.O在BD的垂直平分线上,过O作OD⊥BC于D,由BD=
| 1 |
| 2 |
∵AB是切线,
∴∠ABO=90°,
∴∠ABD+∠OBD=∠BOD+∠OBD=90°,
∴∠ABC=∠BOD,
∴
| BD |
| OB |
| BC |
| AB |
| 4 |
| 5 |
∴OB=
| 5 |
| 2 |
| 5 |
| 2 |
点评:本题考查的是圆的综合题,熟知切线的性质、勾股定理、相似三角形的判定与性质等知识是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
将多项式 3x3-2x2+4x-5添括号后正确的是( )
| A、3x3-(2 x2+4x-5 ) |
| B、( 3x3+4x)-(2 x2+5) |
| C、(3x3-5)+(-2 x2-4x) |
| D、2 x2+(3x3+4x-5) |
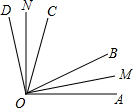 如图所示,OB、OC是∠AOD内的任意两条射线,OM平分∠AOB,ON平分∠COD.若∠AOD=120°,∠BOC=70°.求∠MON使多少度?
如图所示,OB、OC是∠AOD内的任意两条射线,OM平分∠AOB,ON平分∠COD.若∠AOD=120°,∠BOC=70°.求∠MON使多少度? 如图,
如图,