题目内容
如图，在直角梯形ABCD中，AD∥BC，∠BAD=90°，AB=4，CD=5，AD=6，动点P从点A开始以每秒1个单位长度的速度向点B匀速运动，动点Q从点B开始沿折线BC-CD以每秒2个单位长度的速度向点D匀速运动，过点P作PE⊥AB，交CD于点E，设点P、Q同时开始运动，且时间为t秒（t＞0），当点P与点B重合时停止运动，点Q也随之停止运动．（1）BC的长为
（2）当t为何值时，点Q与点E重合？
（3）当点Q在BC上（包括点C）运动时，求S△PQE与t的函数关系式；
（4）当PQ⊥EQ时，请直接写出t的值．
考点：四边形综合题,矩形的判定与性质,平行线分线段成比例,相似三角形的判定与性质
专题：综合题
分析：（1）过点C作CH⊥AD于H，如图1，易证四边形AHCB是矩形，则有CH=AB=4，然后在Rt△CHD中运用勾股定理就可求出HD，进而可求出BC的值．
（2）当点Q与点E重合时，过点C作CH⊥AD于H，如图2，易证△CGQ∽△CHD，然后运用相似三角形的性质就可解决问题．
（3）过点Q作QM⊥PE于M，过点C作CH⊥AD于H，如图3，则有CH=AB=4，QM=CN=BP=4-t．由PE∥AD可得△CNE∽△CHD，然后运用相似三角形的性质用t的代数式表示出NE长，进而表示出PE的长，就可解决问题．
（4）可分点Q在BC上和在CD上两种情况讨论：①若点Q在BC上，过点Q作QM⊥PE于M，过点C作CH⊥AD于H，如图4，表示出QM、PE、MP、ME，然后通过证明△PMQ∽△QME得到MQ2=MP•ME，从而得到关于t的方程，解这个方程就可解决问题；②若点Q在CD上，过点C作CH⊥AD于H，如图5，则有CH=4，PE=
．根据平行线分线段成比例这个性质表示出CE长，进而得到QE长．易证△PQE∽△CHD，然后运用相似三角形的性质建立关于t的方程，解这个方程就可解决问题．
（2）当点Q与点E重合时，过点C作CH⊥AD于H，如图2，易证△CGQ∽△CHD，然后运用相似三角形的性质就可解决问题．
（3）过点Q作QM⊥PE于M，过点C作CH⊥AD于H，如图3，则有CH=AB=4，QM=CN=BP=4-t．由PE∥AD可得△CNE∽△CHD，然后运用相似三角形的性质用t的代数式表示出NE长，进而表示出PE的长，就可解决问题．
（4）可分点Q在BC上和在CD上两种情况讨论：①若点Q在BC上，过点Q作QM⊥PE于M，过点C作CH⊥AD于H，如图4，表示出QM、PE、MP、ME，然后通过证明△PMQ∽△QME得到MQ2=MP•ME，从而得到关于t的方程，解这个方程就可解决问题；②若点Q在CD上，过点C作CH⊥AD于H，如图5，则有CH=4，PE=
| 24-3t |
| 4 |
解答：解：过点C作CH⊥AD于H，如图1．
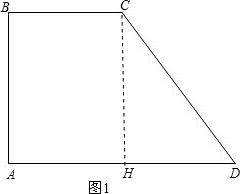
∵∠BAD=90°，CH⊥AD，
∴∠CHD=∠BAD，
∴AB∥CH．
又∵AD∥BC，
∴四边形AHCB是矩形，
∴BC=AH，CH=AB=4．
在Rt△CHD中，
∵∠CHD=90°，CH=4，CD=5，
∴HD=3．
∵AD=6，
∴AH=3，
∴BC=AH=3．
故答案为：3．
（2）当点Q与点E重合时，过点C作CH⊥AD于H，如图2，
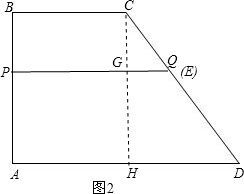
则有CH=AB=4，AP=t，CG=BP=4-t，CQ=2t-3，
∵PE⊥AB，∠BAD=90°，
∴∠BPE=∠BAD=90°，
∴PE∥AD，
∴△CGQ∽△CHD，
∴
=
，
∴
=
，
解得：t=
．
∴当t为
时，点Q与点E重合．
（3）过点Q作QM⊥PE于M，过点C作CH⊥AD于H，如图3．
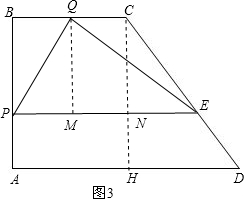
则有CH=AB=4，QM=CN=BP=4-t．
∵PE∥AD，
∴△CNE∽△CHD，
∴
=
，
∴
=
，
∴NE=
，
∴PE=PN+NE=3+
=
，
∴S△PQE=
PE•QM=
×
×（4-t）=
t2-
t+12，（0＜t≤
）．
（4）①若点Q在BC上，过点Q作QM⊥PE于M，过点C作CH⊥AD于H，如图4．
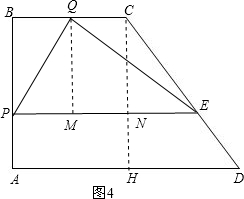
则有CH=AB=4，∠PMQ=∠QME=90°，∠QPM=90°-∠PQM=∠EQM，
QM=BP=4-t，PE=
，MP=QB=2t，ME=PE-PM=
．
∴△PMQ∽△QME，
∴
=
，
∴MQ2=MP•ME，
∴（4-t）2=2t•
，
整理得：13t2-40t+32=0，
△=（-40）2-4×13×32=-64＜0，
方程无解．
②若点Q在CD上，过点C作CH⊥AD于H，如图5．
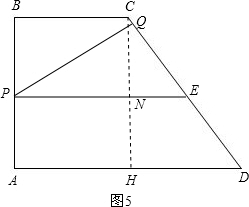
则有CH=4，PE=
．
∵BC∥PE∥AD，
∴∠QEP=∠CDH，
=
，
∴
=
，
∴CE=
．
∵CQ=2t-3，
∴QE=CE-CQ=
-（2t-3）=
，
∵PQ⊥CD，CH⊥AD，
∴∠PQE=∠CHD=90°．
∵∠QEP=∠CDH，∠PQE=∠CHD，
∴△PQE∽△CHD，
∴
=
，
∴CD•QE=HD•PE，
∴5×
=3×
，
解得：t=
．
综上所述：当PQ⊥EQ时，t的值为
．
∵∠BAD=90°，CH⊥AD，
∴∠CHD=∠BAD，
∴AB∥CH．
又∵AD∥BC，
∴四边形AHCB是矩形，
∴BC=AH，CH=AB=4．
在Rt△CHD中，
∵∠CHD=90°，CH=4，CD=5，
∴HD=3．
∵AD=6，
∴AH=3，
∴BC=AH=3．
故答案为：3．
（2）当点Q与点E重合时，过点C作CH⊥AD于H，如图2，
则有CH=AB=4，AP=t，CG=BP=4-t，CQ=2t-3，
∵PE⊥AB，∠BAD=90°，
∴∠BPE=∠BAD=90°，
∴PE∥AD，
∴△CGQ∽△CHD，
∴
| CG |
| CH |
| CQ |
| CD |
∴
| 4-t |
| 4 |
| 2t-3 |
| 5 |
解得：t=
| 32 |
| 13 |
∴当t为
| 32 |
| 13 |
（3）过点Q作QM⊥PE于M，过点C作CH⊥AD于H，如图3．
则有CH=AB=4，QM=CN=BP=4-t．
∵PE∥AD，
∴△CNE∽△CHD，
∴
| CN |
| CH |
| NE |
| HD |
∴
| 4-t |
| 4 |
| NE |
| 3 |
∴NE=
| 12-3t |
| 4 |
∴PE=PN+NE=3+
| 12-3t |
| 4 |
| 24-3t |
| 4 |
∴S△PQE=
| 1 |
| 2 |
| 1 |
| 2 |
| 24-3t |
| 4 |
| 3 |
| 8 |
| 9 |
| 2 |
| 3 |
| 2 |
（4）①若点Q在BC上，过点Q作QM⊥PE于M，过点C作CH⊥AD于H，如图4．
则有CH=AB=4，∠PMQ=∠QME=90°，∠QPM=90°-∠PQM=∠EQM，
QM=BP=4-t，PE=
| 24-3t |
| 4 |
| 24-11t |
| 4 |
∴△PMQ∽△QME，
∴
| MQ |
| ME |
| MP |
| MQ |
∴MQ2=MP•ME，
∴（4-t）2=2t•
| 24-11t |
| 4 |
整理得：13t2-40t+32=0，
△=（-40）2-4×13×32=-64＜0，
方程无解．
②若点Q在CD上，过点C作CH⊥AD于H，如图5．
则有CH=4，PE=
| 24-3t |
| 4 |
∵BC∥PE∥AD，
∴∠QEP=∠CDH，
| CE |
| CD |
| BP |
| BA |
∴
| CE |
| 5 |
| 4-t |
| 4 |
∴CE=
| 20-5t |
| 4 |
∵CQ=2t-3，
∴QE=CE-CQ=
| 20-5t |
| 4 |
| 32-13t |
| 4 |
∵PQ⊥CD，CH⊥AD，
∴∠PQE=∠CHD=90°．
∵∠QEP=∠CDH，∠PQE=∠CHD，
∴△PQE∽△CHD，
∴
| QE |
| HD |
| PE |
| CD |
∴CD•QE=HD•PE，
∴5×
| 32-13t |
| 4 |
| 24-3t |
| 4 |
解得：t=
| 11 |
| 7 |
综上所述：当PQ⊥EQ时，t的值为
| 11 |
| 7 |
点评：本题主要考查了相似三角形的判定与性质、平行线分线段成比例、矩形的判定与性质、根的判别式、勾股定理等知识，有一定的综合性，而运用相似三角形的性质是解决本题的关键．
练习册系列答案
相关题目
如图，已知抛物线y=-x2+3x+4的图象与x轴交于A、B两点，与y轴交于点C，抛物线的对称轴与x轴交于点D、点M从O点出发，以每秒1个单位长度的速度向B点运动（运动到B点停止），过点M作x轴的垂线，交抛物线于点P，交BC与点Q．
如图，平面直角坐标系中，矩形OABC的对角线AC=12，∠ACO=30°
如图，
如图，PA，PB分别切⊙O于点A，B，点E是⊙O上一点，且∠AEB=50°，则∠P=
某校部分团员参加社会公益活动，准备购进一批玩具进行销售，并将所得利润捐给慈善机构．根据市场调查，这种玩具一段时间内的销售量y（个）于销售单价x（元∕个）之间的对应关系如图所示．