题目内容
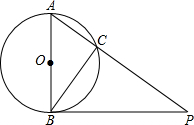如图，已知AB是⊙O的直径，PB是⊙O的切线，PA交⊙O于C，AB=3cm，PB=4cm，则BC长为（ ） | A、5cm | B、2.4cm |
| C、3.6cm | D、1.8cm |
考点：切线的性质
专题：计算题
分析：先根据切线的性质得∠ABP=90°，再在Rt△ABP中利用勾股定理计算出AP=5，接着利用圆周角定理由AB是⊙O的直径得到∠ACB=90°，然后利用面积法求BC的长．
解答：解：∵PB是⊙O的切线，
∴AB⊥PB，
∴∠ABP=90°，
在Rt△ABP中，∵AB=3，PB=4，
∴AP=
=5，
∵AB是⊙O的直径，
∴∠ACB=90°，
∴BC⊥AP，
∵
AB•PB=
BC•AP，
∴BC=
=2.4（cm）．
故选B．
∴AB⊥PB，
∴∠ABP=90°，
在Rt△ABP中，∵AB=3，PB=4，
∴AP=
| AB2+PB2 |
∵AB是⊙O的直径，
∴∠ACB=90°，
∴BC⊥AP，
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴BC=
| 3×4 |
| 5 |
故选B．
点评：本题考查了切线的性质：圆的切线垂直于经过切点的半径．也考查了圆周角定理和三角形面积公式．
练习册系列答案
相关题目
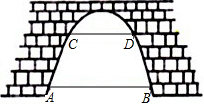如图，有一座抛物线形拱桥，当水位正常时，水面宽度AB为12m，水位上升5m，就达到警戒水位，这时水面宽度CD为8m．
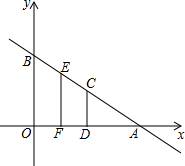如图，平面直角坐标系中，直线AB解析式为：y=
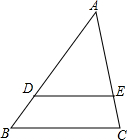如图，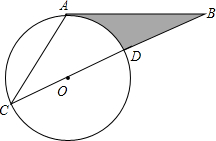
如图所示，AB相切⊙O于点A，直线BO交⊙O于点C、D，且OD=BD，AB=3