题目内容
已知
=
=
,求
的值.
| a+b |
| 11 |
| b+c |
| 10 |
| c+a |
| 15 |
| b+c-a |
| a+b+c |
考点:代数式求值
专题:
分析:令
=
=
=k,则可得一个关于a、b、c的三元一次方程组,求解代入代数式即可求值.
| a+b |
| 11 |
| b+c |
| 10 |
| c+a |
| 15 |
解答:解:令
=
=
=k,则
①+②+③可得:a+b+c=18k④
④-①得c=7k,
④-②得a=8k,
④-③得b=3k,
所以
=
=
=
.
| a+b |
| 11 |
| b+c |
| 10 |
| c+a |
| 15 |
|
①+②+③可得:a+b+c=18k④
④-①得c=7k,
④-②得a=8k,
④-③得b=3k,
所以
| b+c-a |
| a+b+c |
| 3k+7k-8k |
| 18k |
| 2k |
| 18k |
| 1 |
| 9 |
点评:本题主要考查参数法求代数式的值,用一个参数表示出a、b、c的值是解题的关键.

练习册系列答案
相关题目
将多项式 3x3-2x2+4x-5添括号后正确的是( )
| A、3x3-(2 x2+4x-5 ) |
| B、( 3x3+4x)-(2 x2+5) |
| C、(3x3-5)+(-2 x2-4x) |
| D、2 x2+(3x3+4x-5) |
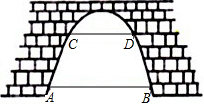 如图,有一座抛物线形拱桥,当水位正常时,水面宽度AB为12m,水位上升5m,就达到警戒水位,这时水面宽度CD为8m.
如图,有一座抛物线形拱桥,当水位正常时,水面宽度AB为12m,水位上升5m,就达到警戒水位,这时水面宽度CD为8m.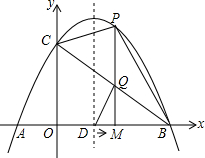 如图,已知抛物线y=-x2+3x+4的图象与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴与x轴交于点D、点M从O点出发,以每秒1个单位长度的速度向B点运动(运动到B点停止),过点M作x轴的垂线,交抛物线于点P,交BC与点Q.
如图,已知抛物线y=-x2+3x+4的图象与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴与x轴交于点D、点M从O点出发,以每秒1个单位长度的速度向B点运动(运动到B点停止),过点M作x轴的垂线,交抛物线于点P,交BC与点Q.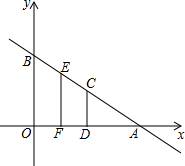 如图,平面直角坐标系中,直线AB解析式为:y=
如图,平面直角坐标系中,直线AB解析式为:y=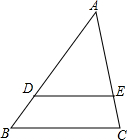 如图,
如图,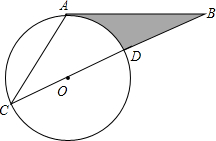 如图所示,AB相切⊙O于点A,直线BO交⊙O于点C、D,且OD=BD,AB=3
如图所示,AB相切⊙O于点A,直线BO交⊙O于点C、D,且OD=BD,AB=3