题目内容
观察下列单项式:
x,-
x2,
x3,-
x4,…-
x19…
(1)写出第100个单项式;
(2)写出第n个单项式.
| 1 |
| 3 |
| 3 |
| 5 |
| 5 |
| 7 |
| 7 |
| 9 |
| 19 |
| 21 |
(1)写出第100个单项式;
(2)写出第n个单项式.
考点:单项式
专题:规律型
分析:(1)观察下列单项式,得出第n项的系数可以表示为(-1)n-1
,指数表示为n,即第n项表示为(-1)n-1
xn.由此可以求得第100个单项式.
(2)根据(1)的规律写出通式即可.
| 2n-1 |
| 2n+1 |
| 2n-1 |
| 2n+1 |
(2)根据(1)的规律写出通式即可.
解答:解:(1)第1个单项式:
x=(-1)1-1•
x,
第2个单项式:-
x2=(-1)2-1•
x2
第3个单项式:
x3=(-1)3-1•
x3,
第4个单项式:-
x4=(-1)4-1•
x4,
…
第100个单项式:(-1)99•
=-
x100…
(2)由(1)的单项式的规律知,第n个单项式为:(-1)n-1
xn.
| 1 |
| 3 |
| 2×1-1 |
| 2×1+1 |
第2个单项式:-
| 3 |
| 5 |
| 2×2-1 |
| 2×2+1 |
第3个单项式:
| 5 |
| 7 |
| 2×3-1 |
| 2×3+1 |
第4个单项式:-
| 7 |
| 9 |
| 2×4-1 |
| 2×4+1 |
…
第100个单项式:(-1)99•
| 2×100-1 |
| 2×100+1 |
| 199 |
| 201 |
(2)由(1)的单项式的规律知,第n个单项式为:(-1)n-1
| 2n-1 |
| 2n+1 |
点评:本题考查的是单项式,根据题意找出规律是解答此题的关键.

练习册系列答案
相关题目
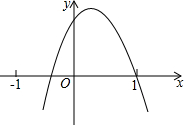 如图,抛物线y=ax2+bx+c的开口向下,交x轴的正半轴于(1,0),则下列结论错误的是( )
如图,抛物线y=ax2+bx+c的开口向下,交x轴的正半轴于(1,0),则下列结论错误的是( )| A、abc<0 |
| B、a-b+c<0 |
| C、2a+b>0 |
| D、a+c<0 |
已知,在△ABC中,∠A=60°,∠C=80°,则∠B=( )
| A、60° | B、30° |
| C、20° | D、40° |
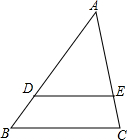 如图,
如图,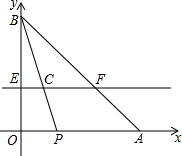 已知Rt△AOB中,OA=8,OB=6,动点P从点A开始在线段AO上以每秒2个单位长度的速度向终点O运动,动直线EF从OA所在位置开始以每秒1个单位长度的速度向上平行移动(即EF∥OA),并且分别与线段OB、AB交于点E、F,连结BP,交直线EF于点C.设动点P与动直线EF同时出发,运动时间为t秒.
已知Rt△AOB中,OA=8,OB=6,动点P从点A开始在线段AO上以每秒2个单位长度的速度向终点O运动,动直线EF从OA所在位置开始以每秒1个单位长度的速度向上平行移动(即EF∥OA),并且分别与线段OB、AB交于点E、F,连结BP,交直线EF于点C.设动点P与动直线EF同时出发,运动时间为t秒.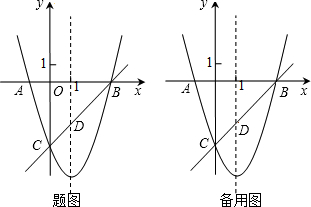
 已知,在正方形ABCD中,⊙O与正方形的边AB、AD相切,对角线BD交⊙O与M、N两点,且MN=2
已知,在正方形ABCD中,⊙O与正方形的边AB、AD相切,对角线BD交⊙O与M、N两点,且MN=2