题目内容
 如图,在Rt△ABC中,CD是斜边AB上的中线,若CD=5,AC=6,则tan∠BCD的值是
如图,在Rt△ABC中,CD是斜边AB上的中线,若CD=5,AC=6,则tan∠BCD的值是考点:锐角三角函数的定义,直角三角形斜边上的中线,勾股定理
专题:
分析:根据直角三角形的性质,可得BA的长,根据勾股定理,可得BC的长,根据三角形的中位线的性质,可得EC、DE的长,根据锐角三角函数正切的定义,可得答案.
解答:解:如图:作DE⊥BC与点E,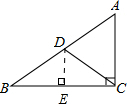 ,
,
由直角三角形的性质,得
AB=2DC=10.
由勾股定理,得
BC=
=8.
由三角形中位线的性质,得
DE=
AC=
×6=3,EC=BE=
BC=4.
由锐角三角函数正切的定义,得
tan∠BCD=
=
,
故答案为:
.
 ,
,由直角三角形的性质,得
AB=2DC=10.
由勾股定理,得
BC=
| AB2-AC2 |
由三角形中位线的性质,得
DE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由锐角三角函数正切的定义,得
tan∠BCD=
| DE |
| EC |
| 3 |
| 4 |
故答案为:
| 3 |
| 4 |
点评:本题考查了锐角三角函数的定义,利用了直角三角形的性质,三角形中位线的性质,锐角三角函数正切的含义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
将多项式 3x3-2x2+4x-5添括号后正确的是( )
| A、3x3-(2 x2+4x-5 ) |
| B、( 3x3+4x)-(2 x2+5) |
| C、(3x3-5)+(-2 x2-4x) |
| D、2 x2+(3x3+4x-5) |
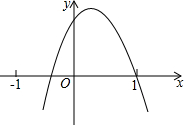 如图,抛物线y=ax2+bx+c的开口向下,交x轴的正半轴于(1,0),则下列结论错误的是( )
如图,抛物线y=ax2+bx+c的开口向下,交x轴的正半轴于(1,0),则下列结论错误的是( )| A、abc<0 |
| B、a-b+c<0 |
| C、2a+b>0 |
| D、a+c<0 |
 如图,
如图,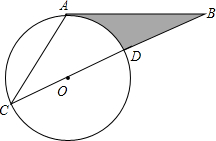 如图所示,AB相切⊙O于点A,直线BO交⊙O于点C、D,且OD=BD,AB=3
如图所示,AB相切⊙O于点A,直线BO交⊙O于点C、D,且OD=BD,AB=3 某校部分团员参加社会公益活动,准备购进一批玩具进行销售,并将所得利润捐给慈善机构.根据市场调查,这种玩具一段时间内的销售量y(个)于销售单价x(元∕个)之间的对应关系如图所示.
某校部分团员参加社会公益活动,准备购进一批玩具进行销售,并将所得利润捐给慈善机构.根据市场调查,这种玩具一段时间内的销售量y(个)于销售单价x(元∕个)之间的对应关系如图所示.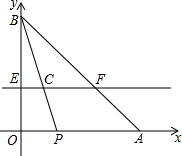 已知Rt△AOB中,OA=8,OB=6,动点P从点A开始在线段AO上以每秒2个单位长度的速度向终点O运动,动直线EF从OA所在位置开始以每秒1个单位长度的速度向上平行移动(即EF∥OA),并且分别与线段OB、AB交于点E、F,连结BP,交直线EF于点C.设动点P与动直线EF同时出发,运动时间为t秒.
已知Rt△AOB中,OA=8,OB=6,动点P从点A开始在线段AO上以每秒2个单位长度的速度向终点O运动,动直线EF从OA所在位置开始以每秒1个单位长度的速度向上平行移动(即EF∥OA),并且分别与线段OB、AB交于点E、F,连结BP,交直线EF于点C.设动点P与动直线EF同时出发,运动时间为t秒.