题目内容
解方程:
(1)x2+4x-2=0 (此题用配方法)
(2)x+3-x(x+3)=0.
(1)x2+4x-2=0 (此题用配方法)
(2)x+3-x(x+3)=0.
考点:解一元二次方程-因式分解法,解一元二次方程-配方法
专题:计算题
分析:(1)方程移项变形后,利用完全平方公式化简,开方即可求出解;
(2)方程左边分解因式后,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解.
(2)方程左边分解因式后,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解.
解答:解:(1)方程变形得:x2+4x=2,
配方得:x2+4x+4=6,即(x+2)2=6,
开方得:x+2=±
,
解得:x1=-2+
,x2=-2-
;
(2)分解因式得:(x+3)(1-x)=0,
可得x+3=0或1-x=0,
解得:x1=-3,x2=1.
配方得:x2+4x+4=6,即(x+2)2=6,
开方得:x+2=±
| 6 |
解得:x1=-2+
| 6 |
| 6 |
(2)分解因式得:(x+3)(1-x)=0,
可得x+3=0或1-x=0,
解得:x1=-3,x2=1.
点评:此题考查了解一元二次方程-因式分解法与配方法,熟练掌握各种解法是解本题的关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
将多项式 3x3-2x2+4x-5添括号后正确的是( )
| A、3x3-(2 x2+4x-5 ) |
| B、( 3x3+4x)-(2 x2+5) |
| C、(3x3-5)+(-2 x2-4x) |
| D、2 x2+(3x3+4x-5) |
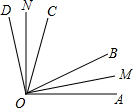 如图所示,OB、OC是∠AOD内的任意两条射线,OM平分∠AOB,ON平分∠COD.若∠AOD=120°,∠BOC=70°.求∠MON使多少度?
如图所示,OB、OC是∠AOD内的任意两条射线,OM平分∠AOB,ON平分∠COD.若∠AOD=120°,∠BOC=70°.求∠MON使多少度?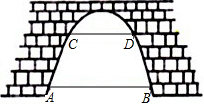 如图,有一座抛物线形拱桥,当水位正常时,水面宽度AB为12m,水位上升5m,就达到警戒水位,这时水面宽度CD为8m.
如图,有一座抛物线形拱桥,当水位正常时,水面宽度AB为12m,水位上升5m,就达到警戒水位,这时水面宽度CD为8m.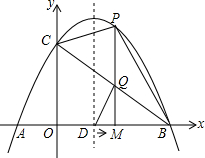 如图,已知抛物线y=-x2+3x+4的图象与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴与x轴交于点D、点M从O点出发,以每秒1个单位长度的速度向B点运动(运动到B点停止),过点M作x轴的垂线,交抛物线于点P,交BC与点Q.
如图,已知抛物线y=-x2+3x+4的图象与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴与x轴交于点D、点M从O点出发,以每秒1个单位长度的速度向B点运动(运动到B点停止),过点M作x轴的垂线,交抛物线于点P,交BC与点Q.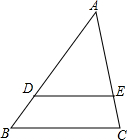 如图,
如图,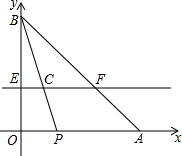 已知Rt△AOB中,OA=8,OB=6,动点P从点A开始在线段AO上以每秒2个单位长度的速度向终点O运动,动直线EF从OA所在位置开始以每秒1个单位长度的速度向上平行移动(即EF∥OA),并且分别与线段OB、AB交于点E、F,连结BP,交直线EF于点C.设动点P与动直线EF同时出发,运动时间为t秒.
已知Rt△AOB中,OA=8,OB=6,动点P从点A开始在线段AO上以每秒2个单位长度的速度向终点O运动,动直线EF从OA所在位置开始以每秒1个单位长度的速度向上平行移动(即EF∥OA),并且分别与线段OB、AB交于点E、F,连结BP,交直线EF于点C.设动点P与动直线EF同时出发,运动时间为t秒.