题目内容
已知方程x2+(2k+1)x+k2-2=0的两实根x1,x2,且有x12+x22=11,求k的值.
考点:根与系数的关系,根的判别式
专题:计算题
分析:先根据判别式的意义得到△=(2k+1)2-4(k2-2)≥0,解得k≥-
,再根据根与系数的关系得到x1+x2=-(2k+1),x1•x2=k2-2,然后已知条件变形为(x1+x2)2-2x1•x2=11,则(2k+1)2-2(k2-2)=11,解方程得k1=-3,k2=1,再利用k的取值范围确定k的值.
| 9 |
| 4 |
解答:解:根据题意得△=(2k+1)2-4(k2-2)≥0,解得k≥-
,
∵x1+x2=-(2k+1),x1•x2=k2-2,
而x12+x22=11,
∴(x1+x2)2-2x1•x2=11,
即(2k+1)2-2(k2-2)=11,
整理得k2+2k-3=0,解得k1=-3,k2=1,
∵k≥-
,
∴k=1.
| 9 |
| 4 |
∵x1+x2=-(2k+1),x1•x2=k2-2,
而x12+x22=11,
∴(x1+x2)2-2x1•x2=11,
即(2k+1)2-2(k2-2)=11,
整理得k2+2k-3=0,解得k1=-3,k2=1,
∵k≥-
| 9 |
| 4 |
∴k=1.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两个为x1,x2,则x1+x2=-
,x1•x2=
.也考查了根的判别式.
| b |
| a |
| c |
| a |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

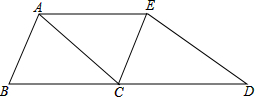 如图.已知在△ABC中AC=BC=10,现将△ABC沿BC方向平移BC得△CDE,
如图.已知在△ABC中AC=BC=10,现将△ABC沿BC方向平移BC得△CDE, 在如图所示的4×2的方格中,∠ACB+∠HCB=
在如图所示的4×2的方格中,∠ACB+∠HCB= 如图,⊙O的直径CD与弦AB交于点M,CD⊥AB,AB=8,CD=10,OM=
如图,⊙O的直径CD与弦AB交于点M,CD⊥AB,AB=8,CD=10,OM=