��Ŀ����
��ͼ��������y=-x2+bx+c������A��4��1������y�ύ�ڵ�B��0��-1����ֱ��l������D��0��-2������ƽ����x�ᣬ����A��AE��l������ΪE��
��1����������ֱ��AB�Ľ���ʽ��
��2������P����ֱ��AB�Ϸ�����������һ�㣬�Ƿ���ڵ�Pʹ�ı���PBDA��������������ڣ�����ı���PBDA����������ֵ���������ʱ��P�����ꣻ��������ڣ���˵�����ɣ�
��3����M���������ڶԳ����ұ߲����ϵ�һ�㣬ֱ��MNƽ����y�ύֱ��AB��N�������M��N��A��EΪ������ı�����ƽ���ı��Σ����M�����꣮
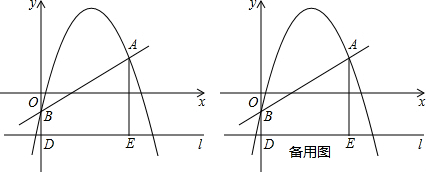
��1����������ֱ��AB�Ľ���ʽ��
��2������P����ֱ��AB�Ϸ�����������һ�㣬�Ƿ���ڵ�Pʹ�ı���PBDA��������������ڣ�����ı���PBDA����������ֵ���������ʱ��P�����ꣻ��������ڣ���˵�����ɣ�
��3����M���������ڶԳ����ұ߲����ϵ�һ�㣬ֱ��MNƽ����y�ύֱ��AB��N�������M��N��A��EΪ������ı�����ƽ���ı��Σ����M�����꣮
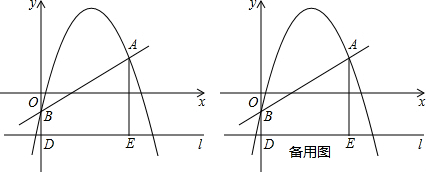
���㣺���κ����ۺ���
ר�⣺ѹ����
��������1���ѵ�A��B��������������߽���ʽ���b��c��ֵ�����ɵý⣻��ֱ��AB�Ľ���ʽΪy=kx+b��k��0����Ȼ�����ô���ϵ������һ�κ�������ʽ��
��2�������ABD������Ƕ�ֵ�жϳ���ABP�����Խ���ı���PBDA�����Խ����P��PF��y�ύAB��F�����P�ĺ�����Ϊx������ֱ�߽���ʽ�������߽���ʽ��ʾ��PF��Ȼ�����S��ABP=S��BPF+S��APF��ʽ�������ٸ��ݶ��κ�������ֵ������
��3�����M�ĺ�����Ϊm�����ݣ�2��д��MN�ı���ʽ���ٸ���ƽ���ı��εĶԱ���ȿɵ�MN=AE��Ȼ��ⷽ�����m���ٴ��������߽���ʽ�����M�������꣬���ɵý⣮
��2�������ABD������Ƕ�ֵ�жϳ���ABP�����Խ���ı���PBDA�����Խ����P��PF��y�ύAB��F�����P�ĺ�����Ϊx������ֱ�߽���ʽ�������߽���ʽ��ʾ��PF��Ȼ�����S��ABP=S��BPF+S��APF��ʽ�������ٸ��ݶ��κ�������ֵ������
��3�����M�ĺ�����Ϊm�����ݣ�2��д��MN�ı���ʽ���ٸ���ƽ���ı��εĶԱ���ȿɵ�MN=AE��Ȼ��ⷽ�����m���ٴ��������߽���ʽ�����M�������꣬���ɵý⣮
����⣺��1����������y=-x2+bx+c������A��4��1����B��0��-1����
��
��
���
��
�������߽���ʽΪy=-x2+
x-1��
��ֱ��AB�Ľ���ʽΪy=kx+b��k��0����
��ֱ��AB������A��4��1����B��0��-1����
��
��
���
��
��ֱ��AB�Ľ���ʽΪy=
x-1��
��2����B��0��-1����D��0��-2����A��4��1����
��BD=-1-��-2��=1����A��BD�ľ���Ϊ4��
��S��ABD=
��1��4=2��
��S�ı���PBDA=S��ABD+S��APB��
���ABP�����Խ���ı���PBDA�����Խ��
����P��PF��y�ύAB��F�����P�ĺ�����Ϊx��
��PF=-x2+
x-1-��
x-1��=-x2+4x��
��S��ABP=S��BPF+S��APF��
=
����-x2+4x����4��
=-2��x-2��2+8��
�൱x=2ʱ��S��ABP�����ֵ8��
x=2ʱ��y=-22+
��2-1=-4+9-1=4��
S�ı���PBDA=S��ABD+S��APB=2+8=10��
�ʴ��ڵ�P��2��4����ʹ�ı���PBDA��������Ϊ10��
��3�����M�ĺ�����Ϊm���ɣ�2��֪MN=-m2+4m��
����M��N��A��EΪ������ı�����ƽ���ı��Σ�
��MN=AE=1-��-2��=3��
��-m2+4m=3��-m2+4m=-3��
�����ã�m2-4m+3=0��m2-4m-3=0
���m1=1��m2=3��m=2��
��
�ߵ�M���������ڶԳ����ұ߲����ϵ�һ�㣬�����ߵĶԳ���Ϊֱ��x=-
=
��
��m��
��
��m=3��m=2+
��
��-32+
��3-1=
��-��2+
��2+
����2+
��-1=-3+
��
����M��N��A��EΪ������ı�����ƽ���ı���ʱ����M������Ϊ��3��
����2+
��-3+
����
��
|
���
|
�������߽���ʽΪy=-x2+
| 9 |
| 2 |
��ֱ��AB�Ľ���ʽΪy=kx+b��k��0����
��ֱ��AB������A��4��1����B��0��-1����
��
|
���
|
��ֱ��AB�Ľ���ʽΪy=
| 1 |
| 2 |
��2����B��0��-1����D��0��-2����A��4��1����
��BD=-1-��-2��=1����A��BD�ľ���Ϊ4��
��S��ABD=
| 1 |
| 2 |

��S�ı���PBDA=S��ABD+S��APB��
���ABP�����Խ���ı���PBDA�����Խ��
����P��PF��y�ύAB��F�����P�ĺ�����Ϊx��
��PF=-x2+
| 9 |
| 2 |
| 1 |
| 2 |
��S��ABP=S��BPF+S��APF��
=
| 1 |
| 2 |
=-2��x-2��2+8��
�൱x=2ʱ��S��ABP�����ֵ8��
x=2ʱ��y=-22+
| 9 |
| 2 |
S�ı���PBDA=S��ABD+S��APB=2+8=10��
�ʴ��ڵ�P��2��4����ʹ�ı���PBDA��������Ϊ10��
��3�����M�ĺ�����Ϊm���ɣ�2��֪MN=-m2+4m��

����M��N��A��EΪ������ı�����ƽ���ı��Σ�
��MN=AE=1-��-2��=3��
��-m2+4m=3��-m2+4m=-3��
�����ã�m2-4m+3=0��m2-4m-3=0
���m1=1��m2=3��m=2��
| 7 |
�ߵ�M���������ڶԳ����ұ߲����ϵ�һ�㣬�����ߵĶԳ���Ϊֱ��x=-
| ||
| 2��(-1) |
| 9 |
| 4 |
��m��
| 9 |
| 4 |
��m=3��m=2+
| 7 |
��-32+
| 9 |
| 2 |
| 7 |
| 2 |
| 7 |
| 9 |
| 2 |
| 7 |
| ||
| 2 |
����M��N��A��EΪ������ı�����ƽ���ı���ʱ����M������Ϊ��3��
| 7 |
| 2 |
| 7 |
| ||
| 2 |
�����������Ƕ��κ����ۺ��⣬��Ҫ�����˴���ϵ��������κ�������ʽ������ϵ������һ�κ�������ʽ�����κ�������ֵ���⣬ƽ���ı��εĶԱ�ƽ�У�����ֱ��AB�Ľ���ʽ�������ߵĽ���ʽ��ʾ��ƽ����y����߶εij����ǽ���Ĺؼ���Ҳ�DZ�����ѵ㣮

��ϰ��ϵ�д�
�����Ŀ