题目内容
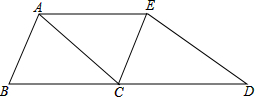 如图.已知在△ABC中AC=BC=10,现将△ABC沿BC方向平移BC得△CDE,
如图.已知在△ABC中AC=BC=10,现将△ABC沿BC方向平移BC得△CDE,(1)四边形CAED是什么特殊的四边形?试说明理由.
(2)当∠ACB=50°时,求四边形CAED的面积.
(供选用数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.2)
(3)当∠ABC为多少度时,四边形CAED是正方形?说明理由.
考点:正方形的判定,菱形的判定,平移的性质,解直角三角形
专题:
分析:(1)根据平移的性质和已知得到AC=DE,BC=CD=AE,AC=BC,推出AC=CD=DE=AE得出四边形CAED是菱形即可;
(2)作EG⊥CD角CD与点G,根据锐角函数的意义求得EG=sin50°•DE,即可求得面积;
(3)四边形CAED是正方形,根据有一个角是直角的菱形是正方形即可判定得出∠ABC为多少度.
(2)作EG⊥CD角CD与点G,根据锐角函数的意义求得EG=sin50°•DE,即可求得面积;
(3)四边形CAED是正方形,根据有一个角是直角的菱形是正方形即可判定得出∠ABC为多少度.
解答:解:(1)四边形ACDE的形状是菱形.
理由是:∵△ABC沿AB方向平移AB长得到△CDE,
∴AC=DE,BC=CD=AE,
∵AC=BC,
∴AC=CD=DE=AE,
∴四边形BDEC为菱形.
(2)如图,

作EG⊥CD角CD与点G,
由平移可知:
∠EDG=∠ACB=50°,
则EG=sin50°•DE=0.77×10=7.7,
S四边形CAED=
CD•EG=38.5.
(3)当∠ABC=90度时,四边形CAED是正方形,
理由:∵四边形ACDE的形状是菱形,∠ABC=90°
∴四边形CAED是正方形.
理由是:∵△ABC沿AB方向平移AB长得到△CDE,
∴AC=DE,BC=CD=AE,
∵AC=BC,
∴AC=CD=DE=AE,
∴四边形BDEC为菱形.
(2)如图,

作EG⊥CD角CD与点G,
由平移可知:
∠EDG=∠ACB=50°,
则EG=sin50°•DE=0.77×10=7.7,
S四边形CAED=
| 1 |
| 2 |
(3)当∠ABC=90度时,四边形CAED是正方形,
理由:∵四边形ACDE的形状是菱形,∠ABC=90°
∴四边形CAED是正方形.
点评:本题主要考查对菱形的判定和性质,平移的性质,正方形的判定,能推出四边形ACDE为菱形是解此题的关键.

练习册系列答案
相关题目
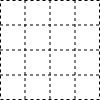 如图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫格点,已知线段AB=5,且端点A、B都在格点,将线段AB向右平移5个单位得到线段DC(点D与点A对应),连接BC、AD,得到四边形ABCD.请你判断这个四边形是哪类特殊的四边形(不需证明,且同类特殊四边形只用画一个),并直接写出四边形的面积.
如图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫格点,已知线段AB=5,且端点A、B都在格点,将线段AB向右平移5个单位得到线段DC(点D与点A对应),连接BC、AD,得到四边形ABCD.请你判断这个四边形是哪类特殊的四边形(不需证明,且同类特殊四边形只用画一个),并直接写出四边形的面积.
 如图,在平面直角坐标系xOy中,直线y=-
如图,在平面直角坐标系xOy中,直线y=-
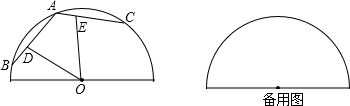
 如图,∠AOD=90°,∠AOB:∠BOC=1:3,OD平分∠BOC,则∠AOC=
如图,∠AOD=90°,∠AOB:∠BOC=1:3,OD平分∠BOC,则∠AOC=