题目内容
15.如图①,在A、B两地之间有汽车站C,客车由A地驶往C站,货车由B地驶往A地.两车同时出发,匀速行驶.图②是客车、货车离C站的路程y1、y2(km)与行驶时间x(h)之间的函数图象.(1)客车的速度是60km/h;
(2)求货车由B地行驶至A地所用的时间;
(3)求点E的坐标,并解释点E的实际意义.
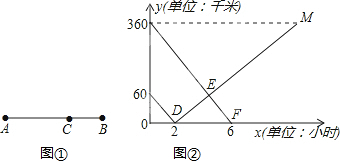
分析 (1)由图象可知客车6小时行驶的路程是360千米,从而可以求得客车的速度;
(2)由图象可以得到货车行驶的总的路程,前2小时行驶的路程是60千米,从而可以起求得货车由B地行驶至A地所用的时间;
(3)根据图象可以分别求得EF和DM所在直线的解析式,然后联立方程组即可求得点E的坐标,根据题意可以得到点E代表的实际意义.
解答 解:(1)由图象可得,
客车的速度是:360÷6=60km/h,
故答案为:60;
(2)由图象可得,
货车由B地到A地的所用的时间是:(60+360)÷(60÷2)=14(小时),
即货车由B地到A地的所用的时间是14小时;
(3)设客车由A到C对应的函数解析式为y=kx+b,
则$\left\{\begin{array}{l}{b=360}\\{6k+b=0}\end{array}\right.$,得$\left\{\begin{array}{l}{k=-60}\\{b=360}\end{array}\right.$,
即客车由A到C对应的函数解析式为y=-60x+360,
货车由C到A对应的函数解析式为y=mx+n,
则$\left\{\begin{array}{l}{2m+n=0}\\{14m+n=360}\end{array}\right.$,得$\left\{\begin{array}{l}{m=30}\\{n=-60}\end{array}\right.$,
即货车由C到A对应的函数解析式为y=30x-60,
∴$\left\{\begin{array}{l}{y=-60x+360}\\{y=30x-60}\end{array}\right.$,得$\left\{\begin{array}{l}{x=\frac{14}{3}}\\{y=80}\end{array}\right.$,
∴点E的坐标为($\frac{14}{3}$,80),点E代表的实际意义是此时客车和货车相遇.
点评 本题考查一次函数的应用,解答此类问题的关键是明确题意,利用一次函数的性质和数形结合的思想解答.

| A. | 赢利16元 | B. | 亏本16元 | C. | 赢利6元 | D. | 亏本6元 |
| A. | 两点之间,线段最短 | B. | 两点确定一条直线 | ||
| C. | 线段的中点定义 | D. | 直线可以向两边延长 |
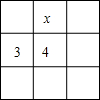 有这样一个数字游戏:将1,2,3,4,5,6,7,8,9这九个数字分别填在如图所示的九个空格中,要求每一行从左到右的数字逐渐增大,每一列从上到下的数字也逐渐增大.当数字3和4固定在图中所示的位置时,x代表的数字是2,此时按游戏规则填写空格,所有可能出现的结果共有6种.
有这样一个数字游戏:将1,2,3,4,5,6,7,8,9这九个数字分别填在如图所示的九个空格中,要求每一行从左到右的数字逐渐增大,每一列从上到下的数字也逐渐增大.当数字3和4固定在图中所示的位置时,x代表的数字是2,此时按游戏规则填写空格,所有可能出现的结果共有6种. 如图,在一个风筝ABCD中,AB=AD,BC=DC,分别在AB、AD的中点E、F处贴两根彩线EC、FC.
如图,在一个风筝ABCD中,AB=AD,BC=DC,分别在AB、AD的中点E、F处贴两根彩线EC、FC.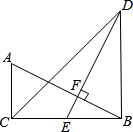 如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE⊥AB,垂足为点F,且AB=DE.
如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE⊥AB,垂足为点F,且AB=DE.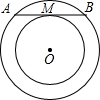 如图,已知两同心圆,大圆的弦AB切小圆于M,若环形的面积为9π,则AB的长是6.
如图,已知两同心圆,大圆的弦AB切小圆于M,若环形的面积为9π,则AB的长是6.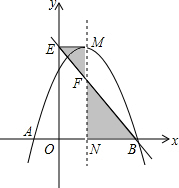 如图,抛物线y=-x2+2x+c与x轴交于A,B两点,它的对称轴与x轴交于点N,过抛物线的顶点M作ME⊥y轴于点E,连接BE交MN于点F,已知点A的坐标为(-1,0).
如图,抛物线y=-x2+2x+c与x轴交于A,B两点,它的对称轴与x轴交于点N,过抛物线的顶点M作ME⊥y轴于点E,连接BE交MN于点F,已知点A的坐标为(-1,0).