题目内容
20．数学源于生活，并用于生活，要把一根木条固定在墙上至少需要钉两颗钉子，其中的数学原理是（ ）| A． | 两点之间，线段最短 | B． | 两点确定一条直线 | ||
| C． | 线段的中点定义 | D． | 直线可以向两边延长 |
分析 根据直线的性质，可得答案．
解答 解：要把一根木条固定在墙上至少需要钉两颗钉子，其中的数学原理是两点确定一条直线，
故选：B．
点评 本题考查了直线的性质，熟记直线的性质是解题关键．
练习册系列答案
期末100分闯关海淀考王系列答案
相关题目
11．关于一元二次方程 x2-2x+3=0 的根的情况正确的是（ ）
| A． | 有两个相等的实数根 | B． | 有两个不相等的实数根 | ||
| C． | 没有实数根 | D． | 不能确定 |
8．下列说法中，正确的有（ ）
| A． | 过两点有无数条直线 | B． | 连结两点的线段叫做两点的距离 | ||
| C． | 两点之间，线段最短 | D． | AB=BC，则点B是线段AC的中点 |
12．
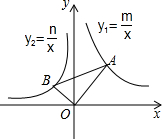如图，在平面直角坐标系中，∠AOB=90°，∠OAB=30°，反比例函数y1=$\frac{m}{x}$的图象经过点A，反比例函数y2=$\frac{n}{x}$的图象经过点B，则下列关于m，n的关系正确的是（ ）
如图，在平面直角坐标系中，∠AOB=90°，∠OAB=30°，反比例函数y1=$\frac{m}{x}$的图象经过点A，反比例函数y2=$\frac{n}{x}$的图象经过点B，则下列关于m，n的关系正确的是（ ）| A． | m=$\frac{\sqrt{3}}{3}$n | B． | m=-$\sqrt{3}$n | C． | m=-$\frac{\sqrt{3}}{3}$n | D． | m=-3n |
9．下列表格是二次函数y=ax2+bx+c（d≠0）的自变量x与函数y的一些对应值，由此可以判断方程ax2+bx+c=0（a≠0）的一个根在（ ）
| x | 6.17 | 6.18 | 6.19 | 6.20 |
| y=ax2+bx+c | -0.03 | -0.01 | 0.02 | 0.06 |
| A． | -0.01-0.02之间 | B． | 0.02-0.06之间 | C． | 6.17-6.18之间 | D． | 6.18-6.19之间 |
