题目内容
7.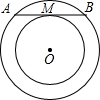 如图,已知两同心圆,大圆的弦AB切小圆于M,若环形的面积为9π,则AB的长是6.
如图,已知两同心圆,大圆的弦AB切小圆于M,若环形的面积为9π,则AB的长是6.
分析 环形的面积为9π,就是大圆面积-小圆的面积,根据圆的面积公式,可得π×OA2-π×OM2=9π,解得OA2-OM2=9,再根据勾股定理可知就是AM的平方,所以AM=3,AB=6.
解答 解:连接OA、OM,如图所示: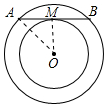
∵大圆的弦AB切小圆于M,
∴AB⊥OM,
∴AM=BM,
∵环形的面积为9π,
根据圆的面积公式可得:π×OA2-π×OM2=9π,
解得:OA2-OM2=9,
根据勾股定理可知:AM2=OA2-OM2,
∴AM=3,
∴AB=2AM=6.
点评 本题考查了切线的性质、垂径定理、勾股定理;做本题的关键是把OA2-OM2=9当成一个整体来计算,并理解9就是AM的平方,从而求出AM,AB的值.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
17.某公司有如表几种手机4G套餐:(1G=1024M)
李老师每月大约使用国内数据流量约800M,国内电话约400分钟,若想使每月付费最少,则应选择的套餐是( )
套餐类型 | 月费(元/月) | 套餐内包含内容 | 套餐外资费 | ||
| 国内数据流量 | 国内电话(分钟) | 流量 | 国内 电话 | ||
| 套餐1 | 76 | 400M | 200 | 0M-200M时,0.3元/M 201M-1G时,60元 | 0.15元/分钟 |
| 套餐2 | 106 | 800M | 300 | ||
| 套餐3 | 136 | 1G | 500 | ||
| 套餐4 | 166 | 2G | 500 | ||
| A. | 套餐1 | B. | 套餐2 | C. | 套餐3 | D. | 套餐4 |
18.下列四个实数中,无理数是( )
| A. | 3.14 | B. | -π | C. | 0 | D. | $\sqrt{4}$ |
12.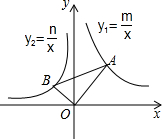 如图,在平面直角坐标系中,∠AOB=90°,∠OAB=30°,反比例函数y1=$\frac{m}{x}$的图象经过点A,反比例函数y2=$\frac{n}{x}$的图象经过点B,则下列关于m,n的关系正确的是( )
如图,在平面直角坐标系中,∠AOB=90°,∠OAB=30°,反比例函数y1=$\frac{m}{x}$的图象经过点A,反比例函数y2=$\frac{n}{x}$的图象经过点B,则下列关于m,n的关系正确的是( )
 如图,在平面直角坐标系中,∠AOB=90°,∠OAB=30°,反比例函数y1=$\frac{m}{x}$的图象经过点A,反比例函数y2=$\frac{n}{x}$的图象经过点B,则下列关于m,n的关系正确的是( )
如图,在平面直角坐标系中,∠AOB=90°,∠OAB=30°,反比例函数y1=$\frac{m}{x}$的图象经过点A,反比例函数y2=$\frac{n}{x}$的图象经过点B,则下列关于m,n的关系正确的是( )| A. | m=$\frac{\sqrt{3}}{3}$n | B. | m=-$\sqrt{3}$n | C. | m=-$\frac{\sqrt{3}}{3}$n | D. | m=-3n |
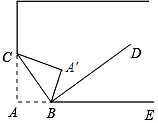 如图,将书角斜折过去,使角顶点落在A′处,BC为折痕,∠A′BD=∠DBE,求∠CBD的度数.
如图,将书角斜折过去,使角顶点落在A′处,BC为折痕,∠A′BD=∠DBE,求∠CBD的度数.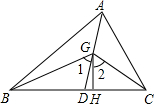 如图,在△ABC中,AD是它的角平分线,G是AD上的一点,BG,CG分别平分∠ABC,∠ACB,GH⊥BC,垂足为H,求证:
如图,在△ABC中,AD是它的角平分线,G是AD上的一点,BG,CG分别平分∠ABC,∠ACB,GH⊥BC,垂足为H,求证: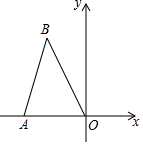 如图,在△ABO中,BA=BO=4,OA=2.则B的坐标是(-1,$\sqrt{15}$).
如图,在△ABO中,BA=BO=4,OA=2.则B的坐标是(-1,$\sqrt{15}$).