题目内容
18.若x,y满足方程组$\left\{\begin{array}{l}{x+y=4}\\{x-2y=1}\end{array}\right.$,则代数式4x2-4xy+y2的值为25.分析 由4x2-4xy+y2分解得(2x-y)2,再将方程组中两方程相加可得2x-y的值,代入即可.
解答 解:方程组$\left\{\begin{array}{l}{x+y=4}&{①}\\{x-2y=1}&{②}\end{array}\right.$中,
①+②,得:2x-y=5,
∴4x2-4xy+y2=(2x-y)2=52=25,
故答案为:25.
点评 本题主要考查方程组的解及代数式的求值,观察待求代数式的特点与方程组中两方程的联系是解题关键.

练习册系列答案
相关题目
8. 如图,在边长为4的菱形ABCD中,∠BAD=120°,则对角线AC的长为( )
如图,在边长为4的菱形ABCD中,∠BAD=120°,则对角线AC的长为( )
 如图,在边长为4的菱形ABCD中,∠BAD=120°,则对角线AC的长为( )
如图,在边长为4的菱形ABCD中,∠BAD=120°,则对角线AC的长为( )| A. | 4 | B. | 2 | C. | 2$\sqrt{3}$ | D. | 3 |
9.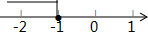 关于x的不等式2x+a≤-3的解集如图所示,则a的取值是( )
关于x的不等式2x+a≤-3的解集如图所示,则a的取值是( )
 关于x的不等式2x+a≤-3的解集如图所示,则a的取值是( )
关于x的不等式2x+a≤-3的解集如图所示,则a的取值是( )| A. | 0 | B. | -1 | C. | -2 | D. | -3 |
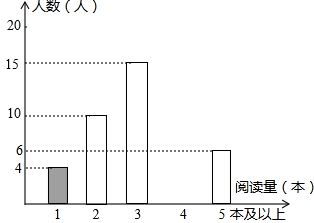 某学校为了解学生的课外阅读情况,王老师随机抽查部分学生,并对其暑假期间的课外阅读量进行统计分析,绘制成如图所示但不完整的统计图.已知抽查的学生在暑假期间阅读量为2本的人数占抽查总人数的20%,根据所给出信息,解答下列问题:
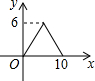
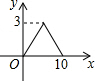
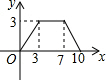
某学校为了解学生的课外阅读情况,王老师随机抽查部分学生,并对其暑假期间的课外阅读量进行统计分析,绘制成如图所示但不完整的统计图.已知抽查的学生在暑假期间阅读量为2本的人数占抽查总人数的20%,根据所给出信息,解答下列问题: 如图,?ABCD中,AB=4,BC=3,∠DCB=30°,动点E从B点出发,沿B-C-D-A运动至A点停止,设运动的路程为x,△ABE的面积为y,则y与x的函数图象用图象表示正确的是( )
如图,?ABCD中,AB=4,BC=3,∠DCB=30°,动点E从B点出发,沿B-C-D-A运动至A点停止,设运动的路程为x,△ABE的面积为y,则y与x的函数图象用图象表示正确的是( )