题目内容
8.解方程组$\left\{\begin{array}{l}{ax+by=2}\\{cx-7y=8}\end{array}\right.$时,某同学把c看错后得到$\left\{\begin{array}{l}{x=-2}\\{y=2}\end{array}\right.$,而正确的解是$\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$,那么a、b、c的值是( )| A. | a=4,b=5,c=2 | B. | a,b,c的值不能确定 | ||
| C. | a=4,b=5,c=-2 | D. | a,b不能确定,c=-2 |
分析 把$\left\{\begin{array}{l}{x=-2}\\{y=2}\end{array}\right.$代入方程ax+by=2求出a-b=-1①,把$\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$代入方程组$\left\{\begin{array}{l}{ax+by=2}\\{cx-7y=8}\end{array}\right.$得出$\left\{\begin{array}{l}{3a-2b=2②}\\{3c+14=8③}\end{array}\right.$解方程组③求出c,解由①②组成的方程组,求出a、b,即可得出选项.
解答 解:把$\left\{\begin{array}{l}{x=-2}\\{y=2}\end{array}\right.$代入方程ax+by=2得:-2a+2b=2,
a-b=-1①,
把$\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$代入方程组$\left\{\begin{array}{l}{ax+by=2}\\{cx-7y=8}\end{array}\right.$得:$\left\{\begin{array}{l}{3a-2b=2②}\\{3c+14=8③}\end{array}\right.$
解方程组③得:c=-2,
解由①②组成的方程组$\left\{\begin{array}{l}{a-b=-1}\\{3a-2b=2}\end{array}\right.$得:a=4,b=5,
故选C.
点评 本题考查了二元一次方程组的解,解二元一次方程组的应用,能理解二元一次方程组解的定义是解此题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | -1-1=0 | B. | 32=6 | C. | -2÷$\frac{1}{2}$=-1 | D. | -33-(-3)3=0 |
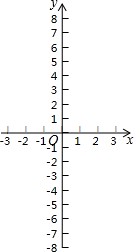 六个函数分别是①y=x;②y=-x+1;③y=x2;④y=-x2+2x-1;⑤y=x3;⑥y=-x3+1.
六个函数分别是①y=x;②y=-x+1;③y=x2;④y=-x2+2x-1;⑤y=x3;⑥y=-x3+1.(1)其中一次函数是①,②,二次函数是③,④,则⑤,⑥的函数可以定义为三次函数;
(2)我们可以借鉴以前研究函数的经验,先探索函数y=x3的图象和性质;
①填写下表,画出函数的图象;
②观察图象,写出该函数两条不同类型的性质;
| x | … | -2 | -$\frac{3}{2}$ | -1 | 0 | 1 | $\frac{3}{2}$ | 2 | … |
| y=x3 | … | … |
(4)函数y=-x3+1的图象关于点(0,1)成中心对称图形.
| A. |  | B. |  | C. |  | D. |  |
| A. | AD=BC,AB∥CD | B. | AO=CO,AD=BC | C. | AD∥BC,∠ADC=∠ABC | D. | AD=BC,∠ABD=∠CDB |
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |

 如图,这是一个十字路口的示意图,机动车从解放西路经过此路口可以直行,也可以左转或右转,假设机动车开往三个方向的可以性是相同的.现有两辆轿车从解放西路驶来经过该路口,求下列事件的概率:
如图,这是一个十字路口的示意图,机动车从解放西路经过此路口可以直行,也可以左转或右转,假设机动车开往三个方向的可以性是相同的.现有两辆轿车从解放西路驶来经过该路口,求下列事件的概率: