题目内容
13．
如图，AB∥CD，∠A=45°，∠C=28°，则∠AEC的大小为（ ）| A． | 17° | B． | 28° | C． | 45° | D． | 73° |
分析 根据两直线平行，内错角相等可得∠ABE=∠C，再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解．
解答 解：如图，∵AB∥CD，
∴∠ABE=∠C=28°，
在△ABE中，由三角形的外角性质得，∠AEC=∠A+∠ABE=45°+28°=73°．
故选D．
点评 本题考查了平行线的性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，熟记各性质并准确识图是解题的关键．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
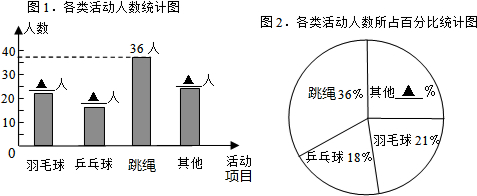
4．
了了解九年级男生的立定跳远成绩，体育老师对该校九年级的260位男生进行了一次立定跳远测试．已知，九年级男生立定跳远成绩（x）的达标要求是：x＜185为不合格；185≤x＜225为合格；x≥225为优秀（单位：cm）．随机以40位男为生的测试数据为样本，绘制出部分频数分布表和部分频数分布直方图，如下所示：
请结合图表完成下列问题：
（1）请把频数分布表和频数分布直方图补充完整；
（2）这个样本数据的中位数落在第几组？
（3）估计该校九年级男生立定跳远成绩为优秀的有多少人？
了了解九年级男生的立定跳远成绩，体育老师对该校九年级的260位男生进行了一次立定跳远测试．已知，九年级男生立定跳远成绩（x）的达标要求是：x＜185为不合格；185≤x＜225为合格；x≥225为优秀（单位：cm）．随机以40位男为生的测试数据为样本，绘制出部分频数分布表和部分频数分布直方图，如下所示：| 组别 | 成绩x（cm） | 频数（人数） |
| 第1组 | 165≤x＜185 | 4 |
| 第2组 | 185≤x＜205 | 6 |
| 第3组 | 205≤x＜225 | |
| 第4组 | 225≤x＜245 | 18 |
| 第5组 | 245≤x＜265 | 4 |
（1）请把频数分布表和频数分布直方图补充完整；
（2）这个样本数据的中位数落在第几组？
（3）估计该校九年级男生立定跳远成绩为优秀的有多少人？
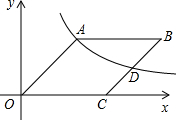如图，O为坐标原点，点C在x轴的正半轴上，四边形OABC是平行四边形，∠AOC=45°，OA=2，反比例函数y=$\frac{k}{x}$在第一现象内的图象经过点A，与BC交于点D．
8．
如图，在边长为4的菱形ABCD中，∠BAD=120°，则对角线AC的长为（ ）
如图，在边长为4的菱形ABCD中，∠BAD=120°，则对角线AC的长为（ ）| A． | 4 | B． | 2 | C． | 2$\sqrt{3}$ | D． | 3 |
18．下列计算中正确的是（ ）
| A． | -1-1=0 | B． | 32=6 | C． | -2÷$\frac{1}{2}$=-1 | D． | -33-（-3）3=0 |
