题目内容
9.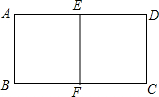 用总长为24米的篱笆围成一个中间隔有一道篱笆的长方形花圃,设AB边长为xm,花圃面积为Sm2.
用总长为24米的篱笆围成一个中间隔有一道篱笆的长方形花圃,设AB边长为xm,花圃面积为Sm2.(1)求S与x之间的函数关系式;
(2)若要使花圃面积为22.5m2,AB长多少米?
(3)当AB长多少米时,花圃的面积最大?最大面积是多少?
分析 (1)可先用篱笆的长表示出BC的长,然后根据矩形的面积=长×宽,得出S与x的函数关系式;
(2)根据(1)的函数关系式,将S=22.5代入其中,求出x的值即可;
(3)根据二次函数的性质求出自变量取值范围内的最值.
解答 解:(1)花圃的宽AB为x米,则BC=$\frac{1}{2}$(24-3x)米,
∴S=$\frac{1}{2}$x(24-3x),
即S=-$\frac{3}{2}$x2+12x(3≤x<8);
(2)当S=22.5时,-$\frac{3}{2}$x2+12x=22.5,
解得x1=3,x2=5,
故AB的长为3米或5米.
(3)S=-$\frac{3}{2}$x2+12x=-$\frac{3}{2}$(x-4)2+24,
∵3≤x<8,
∴当x=4米时面积最大,最大面积为24平方米.
点评 本题考查了二次函数的综合应用,根据已知条件列出二次函数式是解题的关键.要注意题中自变量的取值范围.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
20.函数y=$\frac{1}{{x}^{2}+ax+b}$(a,b为非0常数)取得最大值的条件是( )
| A. | a2-4b≥0 | B. | a2-4b≠0 | ||
| C. | a2-4b<0 | D. | 与a,b取值有关,不能确定 |
20.下列图形中,既是轴对称图形,又是中心对称图形是( )
| A. |  | B. |  | C. |  | D. |  |
17.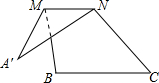 如图,将△ABC沿它的中位线MN折叠后,点A落在点A′处,若∠A′=28°,∠B=120°,则∠A′NC等于( )
如图,将△ABC沿它的中位线MN折叠后,点A落在点A′处,若∠A′=28°,∠B=120°,则∠A′NC等于( )
 如图,将△ABC沿它的中位线MN折叠后,点A落在点A′处,若∠A′=28°,∠B=120°,则∠A′NC等于( )
如图,将△ABC沿它的中位线MN折叠后,点A落在点A′处,若∠A′=28°,∠B=120°,则∠A′NC等于( )| A. | 124° | B. | 92° | C. | 120° | D. | 116° |
4. 如图,在△ABC中,点D、E、F分别在AB、AC、BC边上,DE∥BC,EF∥AB,则下列比例式中错误的是( )
如图,在△ABC中,点D、E、F分别在AB、AC、BC边上,DE∥BC,EF∥AB,则下列比例式中错误的是( )
 如图,在△ABC中,点D、E、F分别在AB、AC、BC边上,DE∥BC,EF∥AB,则下列比例式中错误的是( )
如图,在△ABC中,点D、E、F分别在AB、AC、BC边上,DE∥BC,EF∥AB,则下列比例式中错误的是( )| A. | $\frac{AE}{EC}=\frac{BF}{FC}$ | B. | $\frac{AD}{BF}=\frac{AB}{BC}$ | C. | $\frac{EF}{AB}=\frac{DE}{BC}$ | D. | $\frac{CE}{CF}=\frac{EA}{BF}$ |
1.某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
(1)这批样品的总质量比标准总之多还是少?多或少几克?
(2)若标准质量为45克/袋,则抽样检测的总质量是多少?
(3)这批样品的平均质量比标准质量多还是少?多或少几克?
| 与标准质量的差值(单位:g) | -5 | -2 | 0 | 1 | 3 | 6 |
| 袋数 | 1 | 4 | 3 | 4 | 5 | 3 |
(2)若标准质量为45克/袋,则抽样检测的总质量是多少?
(3)这批样品的平均质量比标准质量多还是少?多或少几克?
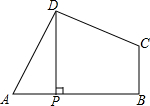 如图所示,四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P,若四边形ABCD的面积是36,求DP的长.
如图所示,四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P,若四边形ABCD的面积是36,求DP的长. 如图,用式子表示圆环的面积.当R=10cm,r=8cm时,求圆环的面积(π取3.14,结果精确到个位).
如图,用式子表示圆环的面积.当R=10cm,r=8cm时,求圆环的面积(π取3.14,结果精确到个位).