题目内容
6．
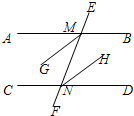如图，AB∥CD，MG平分∠AMN，NH平分∠MND．（1）试猜想MG与NH的位置关系，并说明理由；
（2）试用一句话概括（1）中的结论．
分析 （1）首先根据平行线的性质可得∠AMN=∠DNM，再根据角平分线的性质可得∠1=$\frac{1}{2}$，∠2=$\frac{1}{2}$，再根据等量代换可得∠1=∠2，最后根据内错角相等，两直线平行可得MG∥NH；
（2）根据（1）中的结论用语言叙述结论．
解答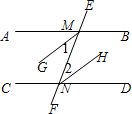 
解：∵AB∥CD，
∴∠AMN=∠DNM （两直线平行，内错角相等），
∵MG平分∠AMN，NH平分∠MND，
∴∠1=$\frac{1}{2}∠$AMF，∠2=$\frac{1}{2}∠$DNE，
∴∠1=∠2），
∴MG∥NH；
（2）如果两直线平行，那么两内错角的平分线也互相平行．
点评 此题主要考查了平行线的判定与性质，角平分线的定义，关键证明∠1=∠2．
练习册系列答案
阅读快车系列答案
相关题目
17．
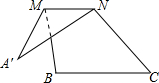如图，将△ABC沿它的中位线MN折叠后，点A落在点A′处，若∠A′=28°，∠B=120°，则∠A′NC等于（ ）
如图，将△ABC沿它的中位线MN折叠后，点A落在点A′处，若∠A′=28°，∠B=120°，则∠A′NC等于（ ）| A． | 124° | B． | 92° | C． | 120° | D． | 116° |
1．某食品厂从生产的袋装食品中抽出样品20袋，检测每袋的质量是否符合标准，超过或不足的部分分别用正、负数来表示，记录如下表：
（1）这批样品的总质量比标准总之多还是少？多或少几克？
（2）若标准质量为45克/袋，则抽样检测的总质量是多少？
（3）这批样品的平均质量比标准质量多还是少？多或少几克？
| 与标准质量的差值（单位：g） | -5 | -2 | 0 | 1 | 3 | 6 |
| 袋数 | 1 | 4 | 3 | 4 | 5 | 3 |
（2）若标准质量为45克/袋，则抽样检测的总质量是多少？
（3）这批样品的平均质量比标准质量多还是少？多或少几克？
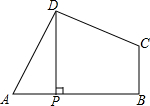如图所示，四边形ABCD中，∠ADC=∠ABC=90°，AD=CD，DP⊥AB于点P，若四边形ABCD的面积是36，求DP的长．
