题目内容
5.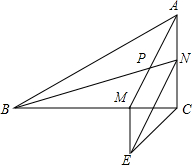 如图,在△ABC中,∠C=90°,AM与BN交于点P,且BM=AC,AN=CM,△EMC是等腰直角三角形,
如图,在△ABC中,∠C=90°,AM与BN交于点P,且BM=AC,AN=CM,△EMC是等腰直角三角形,(1)求证:四边形MENA是平行四边形;
(2)求∠BPM的度数.
分析 (1)首先证明AC∥ME,再证明AN=ME,根据一组对边平行且相等的四边形是平行四边形可得结论;
(2)连接BE,首先证明△BEM≌△AMC,可得∠4=∠AMC,BE=AM,根据平行四边形的性质可得NE=AM,∠2=∠1,AM∥EN,然后可证明△BEN为等腰直角三角形,得到∠BNE=45°,进而可得∠3=∠BPM=45°.
解答 (1)证明:∵△EMC是等腰直角三角形,
∴MC=ME,∠CME=90°,
∵∠C=90°,
∴AC∥ME,
∵AN=CM,
∴AN=ME,
∴四边形MENA是平行四边形;
(2)解:连接BE,
∵四边形AMEN为平行四边形,
∴NE=AM,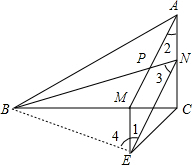 ∠2=∠1,AM∥EN,
∠2=∠1,AM∥EN,
∴∠3=∠BPM,
在△BEM和△AMC中,
$\left\{\begin{array}{l}{MC=ME}\\{∠ACM=∠BME=90°}\\{MB=AC}\end{array}\right.$,
∴△BEM≌△AMC(SAS),
∴∠4=∠AMC,BE=AM,
∵∠2+∠AMC=90°,
∴∠1+∠4=90°,
∵NE=AM,BE=AM,
∴△BEN为等腰直角三角形,∠BNE=45°,
∴∠BPM=∠3=45°.
点评 此题主要考查了平行四边形的性质和判定,关键是正确画出辅助线,构造出全等三角形,掌握平行四边形对边平行且相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
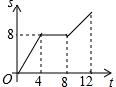
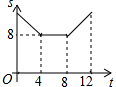
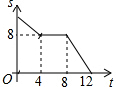
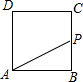 如图,已知正方形ABCD的边长为4,现有一动点P从点B出发,沿着B→C→D→A的路径以每秒1个单位长度的速度运动,则S△PAB与运动时间t(秒)之间的函数关系图象是( )
如图,已知正方形ABCD的边长为4,现有一动点P从点B出发,沿着B→C→D→A的路径以每秒1个单位长度的速度运动,则S△PAB与运动时间t(秒)之间的函数关系图象是( )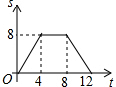
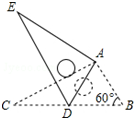 如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若BC=2$\sqrt{3}$,∠B=60°,则CD的长为$\sqrt{3}$.
如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若BC=2$\sqrt{3}$,∠B=60°,则CD的长为$\sqrt{3}$. 已知:如图,AD是△ABC的高,BE平分∠ABC交AD于E,若∠C=70°,∠BED=68°,求∠BAC的度数.
已知:如图,AD是△ABC的高,BE平分∠ABC交AD于E,若∠C=70°,∠BED=68°,求∠BAC的度数.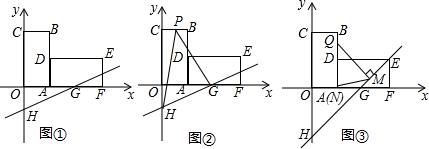
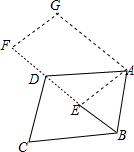 如图,将平行四边形ABCD绕点A旋转到平行四边形AEFG的位置,其中点B、C、D分别落在点E、F、G处,且点B、E、D、F在一直线上,如果点E恰好是对角线BD的中点,那么$\frac{AB}{AD}$的值是$\frac{\sqrt{2}}{2}$.
如图,将平行四边形ABCD绕点A旋转到平行四边形AEFG的位置,其中点B、C、D分别落在点E、F、G处,且点B、E、D、F在一直线上,如果点E恰好是对角线BD的中点,那么$\frac{AB}{AD}$的值是$\frac{\sqrt{2}}{2}$.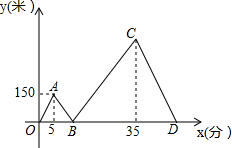 甲、乙两人从学校出发沿同一路线步行到距学校1500米处的图书馆看书,甲与乙在行进过程中以各自的速度匀速行走,甲比乙先出发5分钟,乙比甲先到达图书馆,甲、乙两人间的距离y(米)与甲的行走时间x(分)之间的函数图象如图所示.
甲、乙两人从学校出发沿同一路线步行到距学校1500米处的图书馆看书,甲与乙在行进过程中以各自的速度匀速行走,甲比乙先出发5分钟,乙比甲先到达图书馆,甲、乙两人间的距离y(米)与甲的行走时间x(分)之间的函数图象如图所示.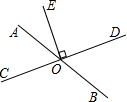 如图,已知直线AB与CD相交于点O,OE⊥CD,则∠AOE与∠DOB互余.
如图,已知直线AB与CD相交于点O,OE⊥CD,则∠AOE与∠DOB互余.