题目内容
2.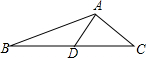 如图△ABC中,点D为BC的中点,AB=5,AC=3,AD=2,则CD长为$\sqrt{13}$.
如图△ABC中,点D为BC的中点,AB=5,AC=3,AD=2,则CD长为$\sqrt{13}$.
分析 延长AD至E,使AD=DE,连接BE,根据SAS证出△ADC≌△BDE,得出BE=AC=3,根据勾股定理的逆定理证出△ABE为RT△,AE⊥BE,再根据勾股定理求出BD,最后根据D为BC的中点,得出BD=CD,从而求出CD.
解答  解:延长AD至E,使AD=DE,连接BE,
解:延长AD至E,使AD=DE,连接BE,
在△ADC和△BDE中,
$\left\{\begin{array}{l}{AD=DE}\\{∠ADC=∠EDB}\\{BD=CD}\end{array}\right.$,
∴△ADC≌△BDE(SAS),
∴BE=AC=3,
∵AE=4,AB=5,32+42=52,
∴△ABE为RT△,AE⊥BE,
∴BD=$\sqrt{B{E}^{2}+E{D}^{2}}$=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,
∵D为BC的中点,
∴BD=CD,
∴CD=$\sqrt{13}$.
故答案为:$\sqrt{13}$.
点评 本题考查了全等三角形的判定与性质,用到的知识点是全等三角形的判定与性质,勾股定理及勾股定理的逆定理,关键是作出辅助线,证出△ADC≌△BDE.

练习册系列答案
相关题目
7. 如图,在△ABC中,AB=AC,∠A=40°,将△ABC绕点B逆时针旋转得到△A′BC′,若点C的对应点C′落在AB边上,则旋转角为( )
如图,在△ABC中,AB=AC,∠A=40°,将△ABC绕点B逆时针旋转得到△A′BC′,若点C的对应点C′落在AB边上,则旋转角为( )
 如图,在△ABC中,AB=AC,∠A=40°,将△ABC绕点B逆时针旋转得到△A′BC′,若点C的对应点C′落在AB边上,则旋转角为( )
如图,在△ABC中,AB=AC,∠A=40°,将△ABC绕点B逆时针旋转得到△A′BC′,若点C的对应点C′落在AB边上,则旋转角为( )| A. | 40° | B. | 70° | C. | 80° | D. | 140° |
 如图,在等边△ABC中,AB=2,N为AB上一点,且AN=1,∠BAC的平分线交BC于点D,M是AD上的动点,连结BM、MN,则BM+MN的最小值是$\sqrt{3}$.
如图,在等边△ABC中,AB=2,N为AB上一点,且AN=1,∠BAC的平分线交BC于点D,M是AD上的动点,连结BM、MN,则BM+MN的最小值是$\sqrt{3}$. 已知:如图,AD是△ABC的高,BE平分∠ABC交AD于E,若∠C=70°,∠BED=68°,求∠BAC的度数.
已知:如图,AD是△ABC的高,BE平分∠ABC交AD于E,若∠C=70°,∠BED=68°,求∠BAC的度数.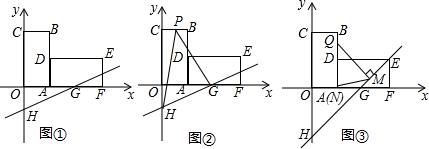
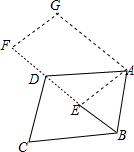 如图,将平行四边形ABCD绕点A旋转到平行四边形AEFG的位置,其中点B、C、D分别落在点E、F、G处,且点B、E、D、F在一直线上,如果点E恰好是对角线BD的中点,那么$\frac{AB}{AD}$的值是$\frac{\sqrt{2}}{2}$.
如图,将平行四边形ABCD绕点A旋转到平行四边形AEFG的位置,其中点B、C、D分别落在点E、F、G处,且点B、E、D、F在一直线上,如果点E恰好是对角线BD的中点,那么$\frac{AB}{AD}$的值是$\frac{\sqrt{2}}{2}$.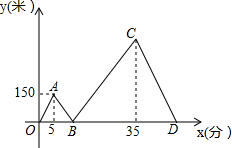 甲、乙两人从学校出发沿同一路线步行到距学校1500米处的图书馆看书,甲与乙在行进过程中以各自的速度匀速行走,甲比乙先出发5分钟,乙比甲先到达图书馆,甲、乙两人间的距离y(米)与甲的行走时间x(分)之间的函数图象如图所示.
甲、乙两人从学校出发沿同一路线步行到距学校1500米处的图书馆看书,甲与乙在行进过程中以各自的速度匀速行走,甲比乙先出发5分钟,乙比甲先到达图书馆,甲、乙两人间的距离y(米)与甲的行走时间x(分)之间的函数图象如图所示. 如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2016,最少经过( )次操作.
如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2016,最少经过( )次操作.