题目内容
2.以[x]表示不超过x的最大整数,如[0.8]=0,[3]=3,则满足二元方程[1.9x]+[8.8y]=36的正整数解的个数为( )| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
分析 显然0≤y≤4(否则等式左边>36),当y=0时,有 x=19.当y=1时,有x=15;当y=2时,x=10;当y=3时,x不存在;当y=4时,x=1.
解答 解:x最小是1,此时[1.9x]=[1.9]=1,此时[8.8y]≤36-1=35,由于8.8×4=35.2,8.8×5=44,所以y≤4,
所以满足[1.9x]+[8.8y]=36的自然数X,Y的值共有4组.
y=0,x=19,
y=1,x=15;
y=2,x=10;
y=3,x无解;
y=4,x=1.
答:满足[1.9x]+[8.8y]=36的自然数x,y的值共有4组.
故选:B.
点评 此题考查一元一次不等式组的实际运用,利用枚举法是解决本题的关键.

练习册系列答案
相关题目
7.若一元二次方程x2-ax-4a=0的两实根之和为4a2-3,则两实根之积为( )
| A. | -4 | B. | 3或-4 | C. | 3 | D. | -3或4 |
 已知△ABC与△DEF都是正三角形,BC与EF的中点都是M.求证:AD⊥CF.
已知△ABC与△DEF都是正三角形,BC与EF的中点都是M.求证:AD⊥CF. 如图,抛物线y=-x2+bx+c经过点A(1,0),C(4,0),与y轴交于点B.
如图,抛物线y=-x2+bx+c经过点A(1,0),C(4,0),与y轴交于点B.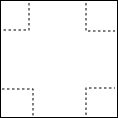 小明用边长为16厘米的正方形纸片制作一个无盖的长方体形纸盒,他在正方形纸片的四个角上剪去边长为4厘米的小正方形(如图),这样折成的无盖长方体纸盒的容积是多少?
小明用边长为16厘米的正方形纸片制作一个无盖的长方体形纸盒,他在正方形纸片的四个角上剪去边长为4厘米的小正方形(如图),这样折成的无盖长方体纸盒的容积是多少?