题目内容
10. 如图,抛物线y=-x2+bx+c经过点A(1,0),C(4,0),与y轴交于点B.
如图,抛物线y=-x2+bx+c经过点A(1,0),C(4,0),与y轴交于点B.(1)求抛物线的解析式;
(2)P是y轴正半轴上一点,且△PAB是以AB为腰的等腰三角形,试求P坐标.
分析 (1)利用待定系数法即可求得抛物线的解析式;
(2)首先求得B的坐标则AB的长即可求得,根据AB是腰,即可求得P的坐标.
解答 解:(1)根据题意得:$\left\{\begin{array}{l}{-1+b+c=0}\\{-16+4b+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=5}\\{c=-4}\end{array}\right.$,
则抛物线的解析式是y=-x2+5x-4;
(2)在y=-x2+5x-4中,令x=0,解得y=-4,
则B的坐标是(0,-4).
则AB=$\sqrt{{1}^{2}+{4}^{2}}$=$\sqrt{17}$,
当A是等腰三角形的顶角顶点时,AP=AB,此时P与B关于x轴对称,则坐标是(0,4);
当B是等腰三角新的顶点时,BP=BA,则OP=$\sqrt{17}$-4,P的坐标是(0,$\sqrt{17}$-4).
总之,P的坐标是(0,$\sqrt{17}$-4)或(0,4).
点评 本题考查了待定系数法求函数解析式,正确进行讨论是关键.

练习册系列答案
相关题目
20.在-2,1,0,7这四个数中,最大的数是( )
| A. | -2 | B. | 1 | C. | 0 | D. | 7 |
15.某班同学在探究弹簧的长度与外力的变化关系时,实验得到相应数据如下表:则y与x的函数图象是( )
| 砝码的质量x(克) | 0 | 50 | 100 | 150 | 200 | 250 | 300 | 400 | 500 | 600 |
| 弹簧的长度y(厘米) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 7.5 | 7.5 | 7.5 |
| A. | 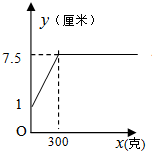 | B. | 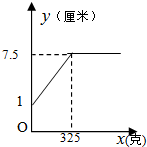 | ||
| C. | 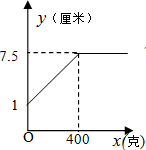 | D. | 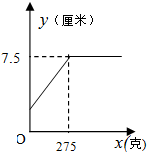 |
20.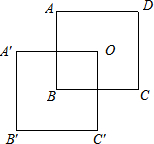 将大小相同的两个正方形纸片按如图所示方式叠放在一起,已知正方形的边长为2,点O为正方形的中心,至少平移几个单位长度才能使两个正方形完全重合?( )
将大小相同的两个正方形纸片按如图所示方式叠放在一起,已知正方形的边长为2,点O为正方形的中心,至少平移几个单位长度才能使两个正方形完全重合?( )
 将大小相同的两个正方形纸片按如图所示方式叠放在一起,已知正方形的边长为2,点O为正方形的中心,至少平移几个单位长度才能使两个正方形完全重合?( )
将大小相同的两个正方形纸片按如图所示方式叠放在一起,已知正方形的边长为2,点O为正方形的中心,至少平移几个单位长度才能使两个正方形完全重合?( )| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
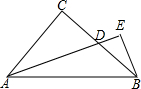 已知:如图,在△ABC中.∠BCA=90°,AC=BC,AE平分∠BAC,BE⊥AE.求证:BE=$\frac{1}{2}$AD.
已知:如图,在△ABC中.∠BCA=90°,AC=BC,AE平分∠BAC,BE⊥AE.求证:BE=$\frac{1}{2}$AD. 如图,D,E分别在△ABC的边BA,CA的延长线上,且DE∥BC,若AB:AD=5:3,则AC:CE的值为5:3.
如图,D,E分别在△ABC的边BA,CA的延长线上,且DE∥BC,若AB:AD=5:3,则AC:CE的值为5:3. 如图所示是一段楼梯,已知AC=5m,CD=7m,楼梯宽BD=5m,一只蚂蚁要从A点爬到B点,求蚂蚁爬行的最短路程.
如图所示是一段楼梯,已知AC=5m,CD=7m,楼梯宽BD=5m,一只蚂蚁要从A点爬到B点,求蚂蚁爬行的最短路程.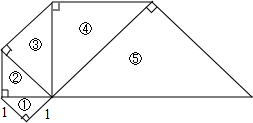 一系列等腰直角三角形组成的螺旋形如图所示,其序号依次为①,②,③,④,⑤,…,则第n等腰直角三角形的斜边长为($\sqrt{2}$)n.
一系列等腰直角三角形组成的螺旋形如图所示,其序号依次为①,②,③,④,⑤,…,则第n等腰直角三角形的斜边长为($\sqrt{2}$)n.