题目内容
7.若一元二次方程x2-ax-4a=0的两实根之和为4a2-3,则两实根之积为( )| A. | -4 | B. | 3或-4 | C. | 3 | D. | -3或4 |
分析 根据根与系数的关系得到a=4a2-3,解得a1=-$\frac{3}{4}$,a2=1,再利用判别式的意义得到a=1,然后再利用根与系数的关系求解.
解答 解:根据题意得a=4a2-3,
整理得4a2-a-3=0,解得a1=-$\frac{3}{4}$,a2=1,
当a=-$\frac{3}{4}$时,x2+$\frac{3}{4}$x+3=0,方程没有实数解,
所以a=1,
所以两实根之积=-4a=-4.
故选A.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
相关题目
15.某班同学在探究弹簧的长度与外力的变化关系时,实验得到相应数据如下表:则y与x的函数图象是( )
| 砝码的质量x(克) | 0 | 50 | 100 | 150 | 200 | 250 | 300 | 400 | 500 | 600 |
| 弹簧的长度y(厘米) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 7.5 | 7.5 | 7.5 |
| A. | 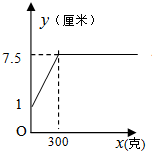 | B. | 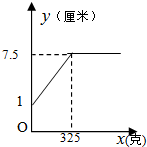 | ||
| C. | 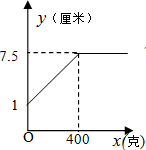 | D. | 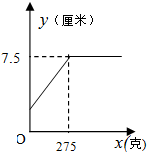 |
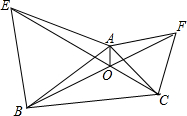 已知△ABC,分别以AB、AC、为边作等边△ABE和等边△ACF,BF与CE交于点O,连接AO,若OA=1,OC=3,OB=4,求线段CE的长.
已知△ABC,分别以AB、AC、为边作等边△ABE和等边△ACF,BF与CE交于点O,连接AO,若OA=1,OC=3,OB=4,求线段CE的长. 如图,D,E分别在△ABC的边BA,CA的延长线上,且DE∥BC,若AB:AD=5:3,则AC:CE的值为5:3.
如图,D,E分别在△ABC的边BA,CA的延长线上,且DE∥BC,若AB:AD=5:3,则AC:CE的值为5:3.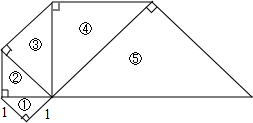 一系列等腰直角三角形组成的螺旋形如图所示,其序号依次为①,②,③,④,⑤,…,则第n等腰直角三角形的斜边长为($\sqrt{2}$)n.
一系列等腰直角三角形组成的螺旋形如图所示,其序号依次为①,②,③,④,⑤,…,则第n等腰直角三角形的斜边长为($\sqrt{2}$)n.