题目内容
17.在△ABC的三个顶点均在⊙O上,且AB=$\sqrt{3}$,AC=$\sqrt{2}$,⊙O的半径为1,求∠BAC的度数.分析 分当AB、AC在圆心O的同侧和AB、AC在圆心O的异侧两种情况进行根据垂径定理和余弦的定义进行解答即可.
解答 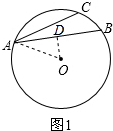 解:当AB、AC在圆心O的同侧时,如图1所示:
解:当AB、AC在圆心O的同侧时,如图1所示:
过点O作OD⊥AB于D,连接OA,
∴AD=$\frac{1}{2}$AB=$\frac{\sqrt{3}}{2}$,OA=1,
∴cos∠OAB=$\frac{AD}{OA}$=$\frac{\sqrt{3}}{2}$.
∴∠OAB=30°,
同理可求:∠OAC=45°,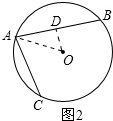 ∴∠BAC=∠OAC-∠OAB=45°-30°=15°;
∴∠BAC=∠OAC-∠OAB=45°-30°=15°;
当AB、AC在圆心O的异侧时,如图2所示:
同理可求:∠OAB=30°,∠OAC=45°.
∴∠BAC=∠OAC+∠OAB=45°+30°=75°.
答:∠BAC的度数为15°或75°.
点评 本题考查的是垂径定理的应用和特殊角的三角函数值的知识,掌握垂直于弦的直径平分弦并且平分弦所对的弧是解题的关键,注意分情况讨论思想的应用.

练习册系列答案
相关题目
6.2009年长春国际动漫艺术节将于2009年5月28日至6月1日在长春市远东艺术馆举行,预计参观人数将超过30万,这个数字用科学记数法表示为( )
| A. | 30×104 | B. | 0.3×106 | C. | 3×105 | D. | 3×104 |
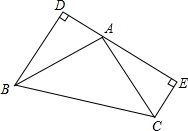 如图,BD⊥DE于D,CE⊥DE于E,AD=CE=2,BD=AE=4.
如图,BD⊥DE于D,CE⊥DE于E,AD=CE=2,BD=AE=4. 如图所示是一段楼梯,已知AC=5m,CD=7m,楼梯宽BD=5m,一只蚂蚁要从A点爬到B点,求蚂蚁爬行的最短路程.
如图所示是一段楼梯,已知AC=5m,CD=7m,楼梯宽BD=5m,一只蚂蚁要从A点爬到B点,求蚂蚁爬行的最短路程.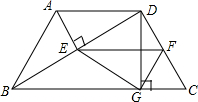 如图,在梯形ABCD中,AD∥BC,AB=DC=AD,∠C=60°,AE⊥BD于点E,F是CD的中点,DG是梯形ABCD的高.则四边形AEFD是什么特殊的四边形?请说明理由.
如图,在梯形ABCD中,AD∥BC,AB=DC=AD,∠C=60°,AE⊥BD于点E,F是CD的中点,DG是梯形ABCD的高.则四边形AEFD是什么特殊的四边形?请说明理由.