题目内容
13. 已知△ABC与△DEF都是正三角形,BC与EF的中点都是M.求证:AD⊥CF.
已知△ABC与△DEF都是正三角形,BC与EF的中点都是M.求证:AD⊥CF.
分析 连接AM,DM,延长AD交CF于点G,由于△ABC和△DEF均为正三角形,BC和EF的中点均为M,于是得到AM⊥BC,DM⊥EF,AM=$\sqrt{3}$CM,DM=$\sqrt{3}$FM,推出△AMD∽△CMF,得到∠MAD=∠MCF,由∠MAD+∠DAC+∠ACM=90°,于是得到∠MCF+∠DAC+∠ACM=90°,即可得到结论.
解答  证明:连接AM,DM,延长AD交CF于点G,
证明:连接AM,DM,延长AD交CF于点G,
∵△ABC和△DEF均为正三角形,BC和EF的中点均为M,
∴AM⊥BC,DM⊥EF,AM=$\sqrt{3}$CM,DM=$\sqrt{3}$FM,
∴∠AMC=∠DMF=90°,
∴∠AMD=∠CMF,AM:DM=CM:FM,
∴△AMD∽△CMF,
∴∠MAD=∠MCF,
∵∠MAD+∠DAC+∠ACM=90°,
∴∠MCF+∠DAC+∠ACM=90°,
∴∠AGC=90°,
∴AD⊥CF.
点评 本题主要考查了相似三角形的判定及性质、等边三角形的性质,本题的关键在于找到需要证相似的三角形,找到对应边的比即可.

练习册系列答案
相关题目
4.已知二次函数y=ax2+bx+c的y与x部分对应值如下表:
则下列判断中正确的是( )
| x | … | -1 | 0 | 1 | 3 | … |
| y | … | -3 | 1 | 3 | 1 | … |
| A. | 抛物线开口向上 | B. | 抛物线与y轴交于负半轴 | ||
| C. | 物线的对称轴为x=1 | D. | 当x=4时,y<0 |
3.某商场于第一年初投入50万元进行商品经营,以后每年年终将当年年初投入资金相加所得的总资金作为下一年年初投入资金继续进行经营,如果第一年的年获利率为P,则第一年年终的总资金可用代数式表示为( )万元.
| A. | 50(1-p) | B. | 50(1+p) | C. | $\frac{50}{1+p}$ | D. | $\frac{50}{1-p}$ |
 将如图所示的围棋盘放在平面直角坐标系内,黑棋A的坐标为(-1.2),黑棋C的坐标为(1,1),那么白棋B的坐标为(-3,-2).
将如图所示的围棋盘放在平面直角坐标系内,黑棋A的坐标为(-1.2),黑棋C的坐标为(1,1),那么白棋B的坐标为(-3,-2).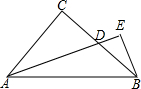 已知:如图,在△ABC中.∠BCA=90°,AC=BC,AE平分∠BAC,BE⊥AE.求证:BE=$\frac{1}{2}$AD.
已知:如图,在△ABC中.∠BCA=90°,AC=BC,AE平分∠BAC,BE⊥AE.求证:BE=$\frac{1}{2}$AD.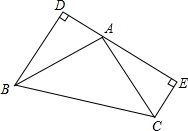 如图,BD⊥DE于D,CE⊥DE于E,AD=CE=2,BD=AE=4.
如图,BD⊥DE于D,CE⊥DE于E,AD=CE=2,BD=AE=4. 如图,D,E分别在△ABC的边BA,CA的延长线上,且DE∥BC,若AB:AD=5:3,则AC:CE的值为5:3.
如图,D,E分别在△ABC的边BA,CA的延长线上,且DE∥BC,若AB:AD=5:3,则AC:CE的值为5:3. 如图所示是一段楼梯,已知AC=5m,CD=7m,楼梯宽BD=5m,一只蚂蚁要从A点爬到B点,求蚂蚁爬行的最短路程.
如图所示是一段楼梯,已知AC=5m,CD=7m,楼梯宽BD=5m,一只蚂蚁要从A点爬到B点,求蚂蚁爬行的最短路程.