题目内容
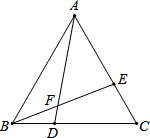如图，△ABC中，AB=AC，D、E分别是BC、AC上的点，AD与BE交于点F．试选取下列条件中的两个作为题设，另一个作为结论组成一个正确命题．①∠BAC=60°；②AE=CD；③∠AFE=60°
（1）题设
（2）求证（1）中命题．
考点：全等三角形的判定与性质,等边三角形的判定与性质,命题与定理
专题：开放型
分析：易证△ABC是等边三角形，即可证明△ABE≌△CAD，可得∠ABE=∠CAD，即可求得∠AFE=∠BAE=60°，即可解题．
解答：证明：（1）题设①②，结论③，
故答案为 ①②，③，；
∵AB=AC，∠BAC=60°，
∴△ABC是等边三角形，
∴∠C=∠BAC=60°，
在△ABE和△CAD中，
，
∴△ABE≌△CAD（SAS），
∴∠ABE=∠CAD，
∵∠CAD+∠AEF+∠ABE=180°，∠ABE+∠AEF+∠AFE=180°，
∴∠AFE=∠BAE=60°．
故答案为 ①②，③，；
∵AB=AC，∠BAC=60°，
∴△ABC是等边三角形，
∴∠C=∠BAC=60°，
在△ABE和△CAD中，
|
∴△ABE≌△CAD（SAS），
∴∠ABE=∠CAD，
∵∠CAD+∠AEF+∠ABE=180°，∠ABE+∠AEF+∠AFE=180°，
∴∠AFE=∠BAE=60°．
点评：本题考查了全等三角形的判定，考查了全等三角形对应角相等的性质，本题中求证△ABE≌△CAD是解题的关键．
练习册系列答案
相关题目
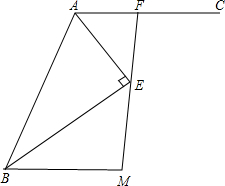如图，AE平分∠BAC，BE⊥AE，AC∥BM，若AB=5，BM=4，求AF的长．
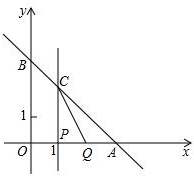已知直线y=-x+3分别交x轴，y轴于A，B两点，线段OA上有一动点P由原点O向点A运动，速度为每秒1个单位长度，过点P作x轴的垂线交直线AB于点C，线段OA上另有一动点Q由点A向点O运动，它与点P以同样速度同时出发，当点P到达点A时两点同时停止运动（如图），设运动时间为t秒．