Question

8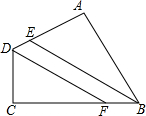．如图，∠A=∠C=90°，BE，DF分别平分∠ABC和∠ADC，求证：BE∥DF．

Answer 1

分析 根据四边形的内角和定理和∠A=∠C=90°，得∠ABC+∠ADC=180°；根据角平分线定义、等角的余角相等易证明和BE与DF两条直线有关的一对同位角相等，从而证明两条直线平行．

解答 证明：∵∠A=∠C=90°（已知），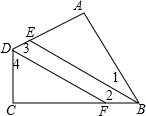

∴∠ABC+∠ADC=180°（四边形的内角和等于360°）．
∵BE平分∠ABC，DF平分∠ADC，
∴∠1=∠2=$\frac{1}{2}$∠ABC，∠3=∠4=$\frac{1}{2}$∠ADC（角平分线的定义）．
∴∠2+∠3=$\frac{1}{2}$（∠ABC+∠ADC）=$\frac{1}{2}$×180°=90°（等式的性质）．
又∠1+∠AEB=90°（三角形的内角和等于180°），
∴∠3=∠AEB（等量代换）．
∴BE∥DF（同位角相等，两直线平行）．

点评 此题主要考查了四边形的内角和定理、角平分线定义、平行线的判定，关键是正确证明∠3=∠CEB．