题目内容
6.下列运算正确的是( )| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | a6÷a2=a3 | C. | (π-3)0=1 | D. | (2a)3=6a3 |
分析 根据二次根式相加减,先把各个二次根式化成最简二次根式,再把被开方数相同的二次根式进行合并,合并方法为系数相加减,根式不变;同底数幂的除法法则:底数不变,指数相减;零指数幂:a0=1(a≠0);幂的乘方法则:底数不变,指数相乘,合并同类项,只把系数相加,字母部分不变进行分析即可.
解答 解:A、$\sqrt{2}$和$\sqrt{3}$不是同类二次根式,不能合并,故原题计算错误;
B、a6÷a2=a4,故原题计算错误;
C、(π-3)0=1,故原题计算正确;
D、(2a)3=8a3,故原题计算错误;
故选:C.
点评 此题主要考查了二次根式的加法、同底数幂除法、幂的乘方,零次幂,关键是掌握各计算法则.

练习册系列答案
相关题目
14.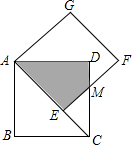 如图,正方形AEFG的边AE放置在正方形ABCD的对角线AC上,EF与CD交于点M,得四边形AEMD,且两正方形的边长均为2,则两正方形重合部分(阴影部分)的面积为( )
如图,正方形AEFG的边AE放置在正方形ABCD的对角线AC上,EF与CD交于点M,得四边形AEMD,且两正方形的边长均为2,则两正方形重合部分(阴影部分)的面积为( )
 如图,正方形AEFG的边AE放置在正方形ABCD的对角线AC上,EF与CD交于点M,得四边形AEMD,且两正方形的边长均为2,则两正方形重合部分(阴影部分)的面积为( )
如图,正方形AEFG的边AE放置在正方形ABCD的对角线AC上,EF与CD交于点M,得四边形AEMD,且两正方形的边长均为2,则两正方形重合部分(阴影部分)的面积为( )| A. | -4+4$\sqrt{2}$ | B. | 4$\sqrt{2}$+4 | C. | 8-4$\sqrt{2}$ | D. | $\sqrt{2}$+1 |
15.声音在空气中传播的速度y(m/s)与气温x(℃)(0≤x≤25)之间的关系如下表:
(1)由上表推出声速y(m/s)随温度x(℃)变化的函数解析式y=$\frac{3}{5}$x+331;
(2)画出函数的图象;
(3)气温在22℃时,有人看到烟花燃放5秒后,才听到声响,那么此人距燃放烟花的所在的地方有1721m.
| 气温x/℃ | 0 | 5 | 10 | 15 | 20 |
| 声速y/m•s-1 | 331 | 334 | 337 | 340 | 343 |
(2)画出函数的图象;
(3)气温在22℃时,有人看到烟花燃放5秒后,才听到声响,那么此人距燃放烟花的所在的地方有1721m.
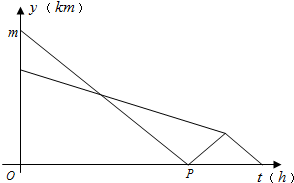 某部队凌晨5:00乘车从住宿地匀速赶往离住宿地90千米的B处执行任务,出发20分钟后在途中遇到提前出发的先遣分队.部队6:00到达B处后,空车原速返回接应先遣分队于6:40准时到达B处.已知汽车和先遣分队距离B处的距离y(km)与汽车行驶时间t(h)的函数关系图象如图所示.
某部队凌晨5:00乘车从住宿地匀速赶往离住宿地90千米的B处执行任务,出发20分钟后在途中遇到提前出发的先遣分队.部队6:00到达B处后,空车原速返回接应先遣分队于6:40准时到达B处.已知汽车和先遣分队距离B处的距离y(km)与汽车行驶时间t(h)的函数关系图象如图所示.
 已知实数a、b、c在数轴上的位置如图所示,a、b到原点的距离相等,化简:$\sqrt{{a}^{2}}$-|a+b|+$\sqrt{(c-a)^{2}}$+|b-c|
已知实数a、b、c在数轴上的位置如图所示,a、b到原点的距离相等,化简:$\sqrt{{a}^{2}}$-|a+b|+$\sqrt{(c-a)^{2}}$+|b-c|