题目内容
5.阅读材料(1),并利用(1)的结论解决问题(2)和问题(3).(1)如图1,AB∥CD,E为形内一点,连结BE、DE得到∠BED,求证:∠E=∠B+∠D.
悦悦是这样做的:
过点E作EF∥AB.则有∠BEF=∠B.
∵AB∥CD,∴EF∥CD.
∴∠FED=∠D.
∴∠BEF+∠FED=∠B+∠D.
即∠BED=∠B+∠D.
(2)如图2,画出∠BEF和∠EFD的平分线,两线交于点G,猜想∠G的度数,并证明你的猜想.
(3)如图3,EG1和EG2为∠BEF内满足∠1=∠2的两条线,分别与∠EFD的平分线交于点G1和G2,求证:∠FG1E+∠G2=180°.
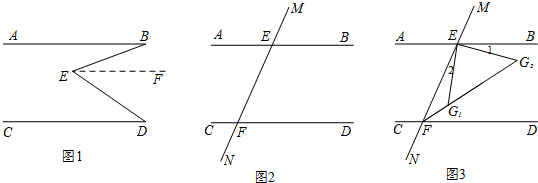
分析 (2)如图2所示,猜想:∠EGF=90°;由结论(1)得∠EGF=∠BEG+∠GFD,根据EG、FG分别平分∠BEF和∠EFD,得到∠BEF=2∠BEG,∠EFD=2∠GFD,由于BE∥CF到∠BEF+∠EFD=180°,于是得到2∠BEG+2∠GFD=180°,即可得到结论;
(3)如图3,过点G1作G1H∥AB由结论(1)可得∠G2=∠1+∠3,∠EG1F=∠BEG1+∠G1FD,得到∠3=∠G2FD,由于FG2平分∠EFD求得∠4=∠G2FD,由于∠1=∠2,于是得到∠G2=∠2+∠4,由于∠EG1F=∠BEG1+∠G1FD,得到∠EG1F+∠G2=∠2+∠4+∠BEG1+∠G1FD=∠BEF+∠EFD,然后根据平行线的性质即可得到结论.
解答 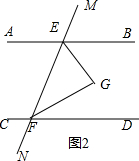 (2)如图2所示,猜想:∠EGF=90°;
(2)如图2所示,猜想:∠EGF=90°;
证明:由结论(1)得∠EGF=∠BEG+∠GFD,
∵EG、FG分别平分∠BEF和∠EFD,
∴∠BEF=2∠BEG,∠EFD=2∠GFD,
∵BE∥CF,
∴∠BEF+∠EFD=180°,
∴2∠BEG+2∠GFD=180°,
∴∠BEG+∠GFD=90°,
∵∠EGF=∠BEG+∠GFD,
∴∠EGF=90°;
(3)证明:如图3,过点G1作G1H∥AB,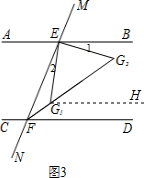
∵AB∥CD,∴G1H∥CD,
由结论(1)可得∠G2=∠1+∠3,∠EG1F=∠BEG1+∠G1FD,
∴∠3=∠G2FD,
∵FG2平分∠EFD,
∴∠4=∠G2FD,
∵∠1=∠2,
∴∠G2=∠2+∠4,
∵∠EG1F=∠BEG1+∠G1FD,
∴∠EG1F+∠G2=∠2+∠4+∠BEG1+∠G1FD=∠BEF+∠EFD,
∵AB∥CD,
∴∠BEF+∠EFD=180°,
∴∠EG1F+∠G2=180°.
点评 本题考查了平行线的性质,角平分线的性质,熟练掌握平行线的性质定理是解题的关键.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案| A. | (1+x)2=2000 | B. | 2000(1+x)2=6600 | ||
| C. | (6600-200)(1+x)=6600 | D. | (6600-2000)(1+x)2=6600 |
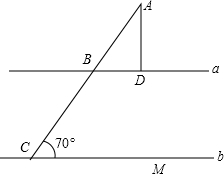 如图所示,已知a∥b,AD⊥直线a,求∠A的度数.
如图所示,已知a∥b,AD⊥直线a,求∠A的度数.