题目内容
14.近年来,全国房价不断上涨,某市201 4年4月份的房价平均每平方米为6600元,比2012年同期的房价平均每平方米上涨了2000元,假设这两年该市房价的平均增长率均为x,则关于x的方程为( )| A. | (1+x)2=2000 | B. | 2000(1+x)2=6600 | ||
| C. | (6600-200)(1+x)=6600 | D. | (6600-2000)(1+x)2=6600 |
分析 设这两年该县房价的平均增长率均为x,那么2013年4月份的房价平均每平方米为(5600-2000)(1+x)元,2014年4月份的房价平均每平方米为(6600-2000)(1+x)(1+x)元,然后根据某县2014年4月份的房价平均每平方米为6600元即可列出方程.
解答 解:∵某县2014年4月份的房价平均每平方米为6600元,比2012年同期的房价平均每平方米上涨了2000元,
∴2012年同期的房价平均每平方米4600元,假设这两年该县房价的平均增长率均为x,
则关于x的方程为:(6600-2000)(1+x)2=6600.
故选D.
点评 本题考查了求平均变化率的方法.若设变化前的量为a,变化后的量为b,平均变化率为x,则经过两次变化后的数量关系为a(1±x)2=b.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
2.下列是二元一次方程的是( )
| A. | 3x-6=x | B. | 3x=2y | C. | 2x+$\frac{3}{y}$=1 | D. | 2x-3y=xy |
9.分式方程$\frac{2x}{x-1}$=3的解为( )
| A. | x=4 | B. | x=3 | C. | x=2 | D. | x=-1 |
19.m为正整数,已知二元一次方程组$\left\{\begin{array}{l}{mx+2y=10}\\{3x-2y=0}\end{array}\right.$有整数解,则m2的值为( )
| A. | 4 | B. | 49 | C. | 4或49 | D. | 1或49 |
6.方程x2+4x-6=0配方后变形为( )
| A. | (x+2)2=10 | B. | (x-2)2=10 | C. | (x+2)2=2 | D. | (x-2)2=2 |
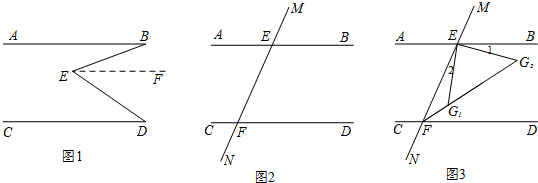
 如图,在两个半圆中,大圆的弦MN与小圆相切,D为切点,且MN∥AB,MN=a,ON、CD分别为两圆的半径,求阴影部分的面积.
如图,在两个半圆中,大圆的弦MN与小圆相切,D为切点,且MN∥AB,MN=a,ON、CD分别为两圆的半径,求阴影部分的面积.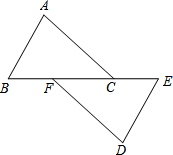 如图,已知点B、F、C、E在同一直线上,AB∥DE,AB=DE,BF=EC,试说明AC与DF平行的理由.
如图,已知点B、F、C、E在同一直线上,AB∥DE,AB=DE,BF=EC,试说明AC与DF平行的理由.