题目内容
4.不解方程,判断方程根的情况:(1)4x2-3x-1=0;
(2)x2-2$\sqrt{2}$x+2=0;
(3)2x2-2x+1=0;
(4)16x2+8x=-3.
分析 (1)(2)(3)直接计算判别式的值,然后根据判别式的意义判断根的情况;
(4)先将方程整理成一般式,再计算判别式的值,然后根据判别式的意义判断根的情况.
解答 解:(1)∵△=(-3)2-4×4×(-1)=25>0,
∴方程有两个不相等实数根;
(2)∵△=(-2$\sqrt{2}$)2-4×1×2=0,
∴方程有两个相等实数根;
(3)∵△=(-2)2-4×2×1=-4<0,
∴方程没有实数根;
(4)将方程整理得:16x2+8x+3=0,
∵△=82-4×16×3=-128<0,
∴方程没有实数根.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2-4ac.当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程没有实数根.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
14.不等式组$\left\{\begin{array}{l}{2x+1<3}\\{4x>1}\end{array}\right.$的解集是( )
| A. | x>1 | B. | x<$\frac{1}{4}$ | C. | $\frac{1}{4}$<x<1 | D. | 无解 |
 如图所示的几何体是由4个相同的小正方体组成,其俯视图为( )
如图所示的几何体是由4个相同的小正方体组成,其俯视图为( )



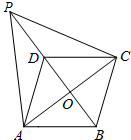 如图,在菱形ABCD中,对角线AC和BD相交于点O,点P是BD延长线上的一点.
如图,在菱形ABCD中,对角线AC和BD相交于点O,点P是BD延长线上的一点.