题目内容
17.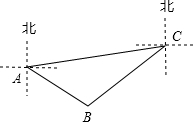 如图,A,B,C分别表示三个小岛上的点,点C在点A的北偏东80°方向,点B在点A的南偏东55°方向,且A,B两点的距离约为6km;同时点B在点C的南偏西50°方向.求A,C两点之间的距离.(结果精确到0.01km.参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{6}$≈2.449)
如图,A,B,C分别表示三个小岛上的点,点C在点A的北偏东80°方向,点B在点A的南偏东55°方向,且A,B两点的距离约为6km;同时点B在点C的南偏西50°方向.求A,C两点之间的距离.(结果精确到0.01km.参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{6}$≈2.449)
分析 直接利用方向角得出各角的度数,进而利用锐角三角函数关系得出AD,DC的长,进而得出答案.
解答 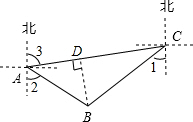 解:过点B作BD⊥AC于点D,
解:过点B作BD⊥AC于点D,
由题意可得:∠2=55°,∠1=50°,∠3=80°,
故∠1+∠2=∠ABC=105°,∠BAC=180°-55°-80°=45°,
则∠ABD=45°,∠DBC=60°,
∵AB=6,
∴AD=BD=AB•sin45°=3$\sqrt{2}$(km),
∴tan60°=$\frac{DC}{DB}$=$\frac{DC}{3\sqrt{2}}$=$\sqrt{3}$,
解得:DC=3$\sqrt{6}$,
则AC=AD+DC=3$\sqrt{2}$+3$\sqrt{6}$≈3(1.414+2.449)≈11.59(km),
答:A,C两点之间的距离为11.59km.
点评 此题主要考查了解直角三角形的应用,正确作出辅助线,得出各角的度数是解题关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
8.若式子$\sqrt{x-1}$在实数范围内有意义,则x的取值范围是( )
| A. | x≠1 | B. | x>1 | C. | x≥1 | D. | x≤1 |
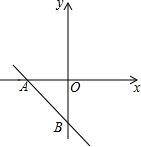 如图,在平面直角坐标系中,一次函数y=-x-3分别与x轴、y轴相交于A、B两点,二次函数y=x2+mx+n(m≠6)的图象经过点A.
如图,在平面直角坐标系中,一次函数y=-x-3分别与x轴、y轴相交于A、B两点,二次函数y=x2+mx+n(m≠6)的图象经过点A.
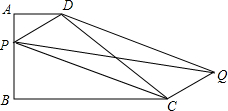 已知梯形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3.
已知梯形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3.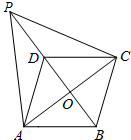 如图,在菱形ABCD中,对角线AC和BD相交于点O,点P是BD延长线上的一点.
如图,在菱形ABCD中,对角线AC和BD相交于点O,点P是BD延长线上的一点.