题目内容
16.若方程组$\left\{\begin{array}{l}{ax+by=2}\\{2x+3y=5}\end{array}\right.$与$\left\{\begin{array}{l}{ax-by=4}\\{4x-5y=-1}\end{array}\right.$的解相同,则a=3,b=-1.分析 联立方程组中不含a与b的方程组成方程组,求出方程组的解得到x与y的值,代入剩下的两方程组成方程组,即可求出a与b的值.
解答 解:由两方程组解相同,联立得:$\left\{\begin{array}{l}{2x+3y=5①}\\{4x-5y=-1②}\end{array}\right.$,
①×2-②得:11y=11,即y=1,
把y=1代入①得:x=1,
把$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$代入得:$\left\{\begin{array}{l}{a+b=2}\\{a-b=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=3}\\{b=-1}\end{array}\right.$.
故答案为:3;-1.
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.

练习册系列答案
相关题目
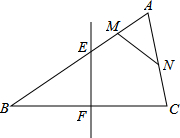 如图,△ABC中,EF是BC边的垂直平分线,M,N分别为AE,AC的中点,求证:MN=$\frac{1}{2}$BE.
如图,△ABC中,EF是BC边的垂直平分线,M,N分别为AE,AC的中点,求证:MN=$\frac{1}{2}$BE.
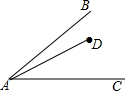 如图,∠BAC=30°,点D在∠BAC的内部,且AD=4cm,请在边AB和AC上确定一点M和N,使得△DMN的周长最小,并求这个最小值.
如图,∠BAC=30°,点D在∠BAC的内部,且AD=4cm,请在边AB和AC上确定一点M和N,使得△DMN的周长最小,并求这个最小值. 如图,一次函数的图象经过点A(0,2)、B(2,-2),写出这个函数的表达式.
如图,一次函数的图象经过点A(0,2)、B(2,-2),写出这个函数的表达式.