题目内容
3.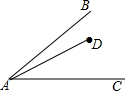 如图,∠BAC=30°,点D在∠BAC的内部,且AD=4cm,请在边AB和AC上确定一点M和N,使得△DMN的周长最小,并求这个最小值.
如图,∠BAC=30°,点D在∠BAC的内部,且AD=4cm,请在边AB和AC上确定一点M和N,使得△DMN的周长最小,并求这个最小值.
分析 作点D关于AB对称的点D1,作点D关于AC对称的点D2,连接D1D2,与AB交于点M,与AC交于点N,此时△DMN的周长最小,然后根据∠BAC=30°,求得∠D1AD2=60°,进而证得△AD1D2是等边三角形.从而求得D1D2=AD1=AD=4cm.
解答 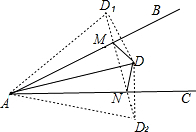 解:作点D关于AB对称的点D1,作点D关于AC对称的点D2,连接D1D2,与AB交于点M,与AC交于点N,此时△DMN的周长最小.
解:作点D关于AB对称的点D1,作点D关于AC对称的点D2,连接D1D2,与AB交于点M,与AC交于点N,此时△DMN的周长最小.
从图上可看出△PEF的周长就是D1D2的长,
∵∠BAC=30°,
∴∠D1AD2=60°.
∵AD1=AD2,
∴△AD1D2是等边三角形.
∴D1D2=AD1=AD=4cm.
△DMN的周长最小值是4cm.
点评 此题主要考查了轴对称最短路径问题,关键是确定M,N的位置,然后找到最小周长的三角形,然后求出最小周长.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
 如图,在矩形ABCD中,AB=1,AD=2,将AD绕点A顺时针旋转,当点D落在BC上点D′时,则∠DAD′=30度.
如图,在矩形ABCD中,AB=1,AD=2,将AD绕点A顺时针旋转,当点D落在BC上点D′时,则∠DAD′=30度.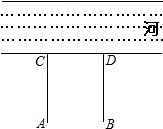 如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD,且AC=BD.若A到河岸CD的中点的距离为500米.
如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD,且AC=BD.若A到河岸CD的中点的距离为500米.