题目内容
3. 如图,AB是⊙O的直径,弦CD⊥AB于H,若BH=2,CD=8,则⊙O的半径长为( )
如图,AB是⊙O的直径,弦CD⊥AB于H,若BH=2,CD=8,则⊙O的半径长为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 先根据垂径定理求出CH的长,设⊙O的半径为r,再连接OC,在Rt△OCH中利用勾股定理求出r的值即可.
解答  解:连接OC,
解:连接OC,
∵⊙O的弦CD=8,半径CD⊥AB,
∴CH=$\frac{1}{2}$CD=$\frac{1}{2}$×8=4,
设⊙O的半径为r,则OH=r-BH=r-2,
在Rt△OCH中,
OC2=OH2+CH2,即r2=(r-2)2+42,解得r=5.
故选D.
点评 本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14. 如图,已知点A(0,1),B(0,-1),以点A为圆心,AB为半径作圆,交x轴的正半轴于点C,则∠BAC等于( )
如图,已知点A(0,1),B(0,-1),以点A为圆心,AB为半径作圆,交x轴的正半轴于点C,则∠BAC等于( )
 如图,已知点A(0,1),B(0,-1),以点A为圆心,AB为半径作圆,交x轴的正半轴于点C,则∠BAC等于( )
如图,已知点A(0,1),B(0,-1),以点A为圆心,AB为半径作圆,交x轴的正半轴于点C,则∠BAC等于( )| A. | 90° | B. | 120° | C. | 60° | D. | 30° |
11.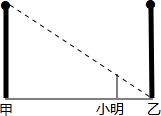 如图,甲、乙两盏路灯杆相距20米,一天晚上,当小明从灯甲底部向灯乙底部直行16米时,发现自己的身影顶部正好接触到路灯乙的底部.已知小明的身高为1.6米,那么路灯甲的高为( )
如图,甲、乙两盏路灯杆相距20米,一天晚上,当小明从灯甲底部向灯乙底部直行16米时,发现自己的身影顶部正好接触到路灯乙的底部.已知小明的身高为1.6米,那么路灯甲的高为( )
 如图,甲、乙两盏路灯杆相距20米,一天晚上,当小明从灯甲底部向灯乙底部直行16米时,发现自己的身影顶部正好接触到路灯乙的底部.已知小明的身高为1.6米,那么路灯甲的高为( )
如图,甲、乙两盏路灯杆相距20米,一天晚上,当小明从灯甲底部向灯乙底部直行16米时,发现自己的身影顶部正好接触到路灯乙的底部.已知小明的身高为1.6米,那么路灯甲的高为( )| A. | 7米 | B. | 8米 | C. | 9米 | D. | 10米 |
8.要使(x2+ax+1)(-6x3)的展开式中不含x4项,则a应等于( )
| A. | 6 | B. | -1 | C. | $\frac{1}{6}$ | D. | 0 |
15.若x2-y2=8,x+y=-4,则x-y的值是( )
| A. | 4 | B. | -4 | C. | 2 | D. | -2 |
 如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接AD,若△ABC的周长为24,AB=7,则△ADC的周长为( )
如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接AD,若△ABC的周长为24,AB=7,则△ADC的周长为( )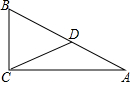 如图,在Rt△ABC中,∠C=90°,D为AB上的点,BD=CD=5,则AD=5.
如图,在Rt△ABC中,∠C=90°,D为AB上的点,BD=CD=5,则AD=5.