题目内容
17.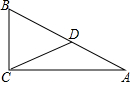 如图,在Rt△ABC中,∠C=90°,D为AB上的点,BD=CD=5,则AD=5.
如图,在Rt△ABC中,∠C=90°,D为AB上的点,BD=CD=5,则AD=5.
分析 由BD=DC,推出∠B=∠DCB,由∠B+∠A=90°,∠DCB+∠DCA=90°,推出∠A=∠DCA,可得AD=DC=5.
解答 解:在Rt△ABC中,∠C=90°,
∵BD=DC,
∴∠B=∠DCB,
∵∠B+∠A=90°,∠DCB+∠DCA=90°,
∴∠A=∠DCA,
∴AD=DC=5,
故答案为5.
点评 本题考查等腰三角形的性质和判定、直角三角形的性质等知识,解题的关键是利用的等角的余角相等解决问题,属于中考常考题型.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
3. 如图,AB是⊙O的直径,弦CD⊥AB于H,若BH=2,CD=8,则⊙O的半径长为( )
如图,AB是⊙O的直径,弦CD⊥AB于H,若BH=2,CD=8,则⊙O的半径长为( )
 如图,AB是⊙O的直径,弦CD⊥AB于H,若BH=2,CD=8,则⊙O的半径长为( )
如图,AB是⊙O的直径,弦CD⊥AB于H,若BH=2,CD=8,则⊙O的半径长为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
2.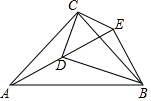 如图,已知△ABC是等腰直角三角形,其内部有一点D,连接BD,以BD为斜边作等腰直角三角形BDE,连接AD、CD、CE,若CD=1,AD=2,∠DCE=90°,则DE的长是 ( )
如图,已知△ABC是等腰直角三角形,其内部有一点D,连接BD,以BD为斜边作等腰直角三角形BDE,连接AD、CD、CE,若CD=1,AD=2,∠DCE=90°,则DE的长是 ( )
 如图,已知△ABC是等腰直角三角形,其内部有一点D,连接BD,以BD为斜边作等腰直角三角形BDE,连接AD、CD、CE,若CD=1,AD=2,∠DCE=90°,则DE的长是 ( )
如图,已知△ABC是等腰直角三角形,其内部有一点D,连接BD,以BD为斜边作等腰直角三角形BDE,连接AD、CD、CE,若CD=1,AD=2,∠DCE=90°,则DE的长是 ( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
9.在直角坐标系中,⊙A的半径为5厘米,圆心A的坐标为(-1,4),点P(3,-1)与⊙A的位置关系是( )
| A. | 在圆上 | B. | 在圆内 | C. | 在圆外 | D. | 无法确定 |
7.已知⊙A的半径长为2,⊙B的半径长为5,如果⊙A与⊙B内含,那么圆心距AB的长度可以为( )
| A. | 0 | B. | 3 | C. | 6 | D. | 9 |
 工人师傅盖房子时,常将房梁设计如图所示的图形,使其牢固不变形,这是利用三角形稳定性.
工人师傅盖房子时,常将房梁设计如图所示的图形,使其牢固不变形,这是利用三角形稳定性.
 如图,⊙O中,直径AB与弦CD相交,E是AC延长线上一点,连接BC、BD,且∠EBC=∠D.
如图,⊙O中,直径AB与弦CD相交,E是AC延长线上一点,连接BC、BD,且∠EBC=∠D.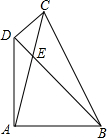 如图,在四边形ABCD中,对角线AC、BD相交于点E,∠DAB=∠CDB=90°,∠ABD=45°,∠DCA=30°,AB=6,则AE=2$\sqrt{6}$.
如图,在四边形ABCD中,对角线AC、BD相交于点E,∠DAB=∠CDB=90°,∠ABD=45°,∠DCA=30°,AB=6,则AE=2$\sqrt{6}$.