题目内容
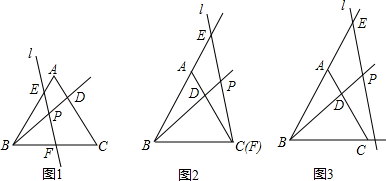
 如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E.
如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E.(1)若∠B=30°,∠ACB=80°,求∠E的度数;
(2)当P点在线段AD上运动时,猜想∠E与∠B、∠ACB的数量关系,写出结论无需证明.
考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)首先根据三角形的内角和定理求得∠BAC的度数,再根据角平分线的定义求得∠DAC的度数,从而根据三角形的内角和定理即可求出∠ADC的度数,进一步求得∠E的度数;
(2)根据第(1)小题的思路即可推导这些角之间的关系.
(2)根据第(1)小题的思路即可推导这些角之间的关系.
解答:解:(1)∵∠B=30°,∠ACB=80°,
∴∠BAC=70°,
∵AD平分∠BAC,
∴∠DAC=35°,
∴∠ADC=65°,
∴∠E=25°;
(2)∠E=
(∠ACB-∠B).
设∠B=n°,∠ACB=m°,
∵AD平分∠BAC,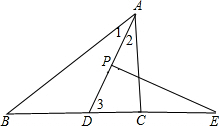
∴∠1=∠2=
∠BAC,
∵∠B+∠ACB+∠BAC=180°,
∵∠B=n°,∠ACB=m°,
∴∠CAB=(180-n-m)°,
∴∠BAD=
(180-n-m)°,
∴∠3=∠B+∠1=n°+
(180-n-m)°=90°+
n°-
m°,
∵PE⊥AD,
∴∠DPE=90°,
∴∠E=90°-(90°+
n°-
m°)=
(m-n)°=
(∠ACB-∠B).
∴∠BAC=70°,
∵AD平分∠BAC,
∴∠DAC=35°,
∴∠ADC=65°,
∴∠E=25°;
(2)∠E=
| 1 |
| 2 |
设∠B=n°,∠ACB=m°,
∵AD平分∠BAC,

∴∠1=∠2=
| 1 |
| 2 |
∵∠B+∠ACB+∠BAC=180°,
∵∠B=n°,∠ACB=m°,
∴∠CAB=(180-n-m)°,
∴∠BAD=
| 1 |
| 2 |
∴∠3=∠B+∠1=n°+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵PE⊥AD,
∴∠DPE=90°,
∴∠E=90°-(90°+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查三角形的内角和定理以及角平分线的定义.掌握三角形的内角和为180°,以及角平分线的性质是解决问题的关键.

练习册系列答案
相关题目
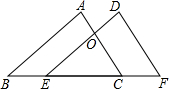 已知,如图,点B、E、C、F四点在同一条直线上,AB∥DE,AB=DE,AC、DE相交于点O,BE=CF.求证:AC=DF.
已知,如图,点B、E、C、F四点在同一条直线上,AB∥DE,AB=DE,AC、DE相交于点O,BE=CF.求证:AC=DF. 如图,AB=AC,BD⊥AC,CE⊥AB,垂足分别为D,E,BD,CE相交于点F,BE与CD相等吗?请说明理由.
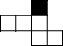
如图,AB=AC,BD⊥AC,CE⊥AB,垂足分别为D,E,BD,CE相交于点F,BE与CD相等吗?请说明理由. 如图,它需再添一个面,折叠后才能围成一个正方体.图中的黑色小正方形分别由四位同学补画,其中正确的是( )
如图,它需再添一个面,折叠后才能围成一个正方体.图中的黑色小正方形分别由四位同学补画,其中正确的是( )

 如图,将甲图经过
如图,将甲图经过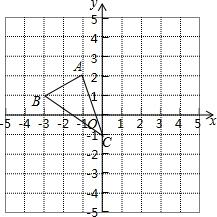 在直角坐标系中,△ABC的顶点坐标是A(-1,2)、B(-3,1)、C(0,-1).
在直角坐标系中,△ABC的顶点坐标是A(-1,2)、B(-3,1)、C(0,-1).