题目内容
7. 在Rt△ABC中,已知∠C=90°,∠A=30°,BC=3,求AB、AC.
在Rt△ABC中,已知∠C=90°,∠A=30°,BC=3,求AB、AC.
分析 先利用含30度直角三角形的性质得到AB=2BC,求出AB的长,再利用勾股定理求出AC的长即可.
解答 解:在Rt△ABC中,∠C=90°,∠A=30°,BC=3,
∴AB=2BC=6,
根据勾股定理得:AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$.
点评 此题考查了勾股定理,以及含30度直角三角形的性质,熟练掌握勾股定理是解本题的关键.

练习册系列答案
相关题目
18.如图,在数轴上表示-1≤x<3正确的是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
2.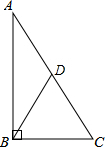 如图,在直角三角形ABC中,两直角边边长分别为6cm和8cm,则连接顶点B与斜边中点D的线段长为( )
如图,在直角三角形ABC中,两直角边边长分别为6cm和8cm,则连接顶点B与斜边中点D的线段长为( )
 如图,在直角三角形ABC中,两直角边边长分别为6cm和8cm,则连接顶点B与斜边中点D的线段长为( )
如图,在直角三角形ABC中,两直角边边长分别为6cm和8cm,则连接顶点B与斜边中点D的线段长为( )| A. | 10cm | B. | 3cm | C. | 4cm | D. | 5cm |
12.下列说法中不正确的是( )
| A. | 三边长为a、b、c,满足a2-b2=c2的三角形是直角三角形 | |
| B. | 三个角度之比为1:1:$\sqrt{2}$的三角形是直角三角形 | |
| C. | 三个角度之比为1:2:3的三角形是直角三角形 | |
| D. | 三边之比为1:2:$\sqrt{3}$的三角形是直角三角形 |
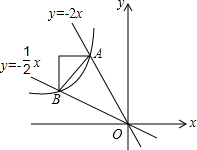 如图,直线y=-2x,y=-$\frac{1}{2}$x交双曲线y=$\frac{k}{x}$于A,B两点(x<0)且S△OAB=4,求k.
如图,直线y=-2x,y=-$\frac{1}{2}$x交双曲线y=$\frac{k}{x}$于A,B两点(x<0)且S△OAB=4,求k. 如图,∠1=∠2,∠3=35°,则∠4=145°.
如图,∠1=∠2,∠3=35°,则∠4=145°. 如图,在△ABC中,AB=AC,D、E、F分别在三边上,且BE=CD,BD=CF,G为EF的中点.
如图,在△ABC中,AB=AC,D、E、F分别在三边上,且BE=CD,BD=CF,G为EF的中点.