题目内容
17.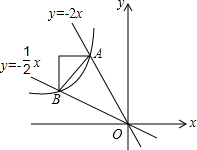 如图,直线y=-2x,y=-$\frac{1}{2}$x交双曲线y=$\frac{k}{x}$于A,B两点(x<0)且S△OAB=4,求k.
如图,直线y=-2x,y=-$\frac{1}{2}$x交双曲线y=$\frac{k}{x}$于A,B两点(x<0)且S△OAB=4,求k.
分析 认真审题,过点B作BD⊥x轴,垂足为D,过点A作AC⊥x轴,用四边形ABDO的面积减去三角形BOD的面积,即为三角形OAB的面积,进而得解.
解答 解:如图,过点B作BD⊥x轴,垂足为D,过点A作AC⊥x轴,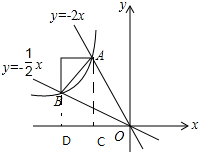
∴BD∥AC,
设A(m,$\frac{k}{m}$),B(n,$\frac{k}{n}$),
则:BD=$\frac{k}{n}$,AC=$\frac{k}{m}$,CD=m-n,
梯形ABDC的面积为:$\frac{1}{2}$×(m-n)×($\frac{k}{m}+\frac{k}{n}$),S△AOC=$\frac{|k|}{2}$,${S}_{△BOD}=\frac{|k|}{2}$,
∴$\frac{1}{2}$×(m-n)×($\frac{k}{m}+\frac{k}{n}$)+$\frac{|k|}{2}$-$\frac{|k|}{2}$=4,
即:$\frac{({m}^{2}-{n}^{2})k}{mn}$=8,
由$\left\{\begin{array}{l}{y=-2x}\\{y=\frac{k}{x}}\end{array}\right.$可知m2=$-\frac{k}{2}$,由$\left\{\begin{array}{l}{y=-\frac{1}{2}x}\\{y=\frac{k}{x}}\end{array}\right.$可知n2=-2k,
∴m2n2=k2,∴mn=-k,
∴$\frac{(-\frac{k}{2}+2k)k}{-k}$=8,
解得:k=$-\frac{16}{3}$.
点评 本题主要考查了反比例函数与一次函数的交点的问题,利用含有k的代数式表示出△AOB的面积是解题的关键,注意运算过程的简化,认真总结.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
5.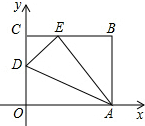 如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,则点D的坐标为( )
如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,则点D的坐标为( )
 如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,则点D的坐标为( )
如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,则点D的坐标为( )| A. | (0,3) | B. | (0,4) | C. | (0,5) | D. | (0,6) |
2.在Rt△ABC中,∠C=90°,AB:AC=2:1,则∠A的度数是( )
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
9.下列运算中,结果是a18的是( )
| A. | a9+a9 | B. | a3•a6 | C. | (a3)6 | D. | (a2•a3)3 |
 如图,已知点A(m-5,m)和点B(m-2,m-4.5)是一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(k≠0,x>0)图象的两个交点,AC⊥y轴于C,BD⊥x轴于D.
如图,已知点A(m-5,m)和点B(m-2,m-4.5)是一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(k≠0,x>0)图象的两个交点,AC⊥y轴于C,BD⊥x轴于D.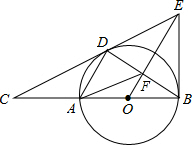 如图,点D是半径为5的⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD,CA=8,过点B作⊙O的切线BE交直线CD于点E,连接AD、BD、OE的交点是F,连接AF.
如图,点D是半径为5的⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD,CA=8,过点B作⊙O的切线BE交直线CD于点E,连接AD、BD、OE的交点是F,连接AF. 在Rt△ABC中,已知∠C=90°,∠A=30°,BC=3,求AB、AC.
在Rt△ABC中,已知∠C=90°,∠A=30°,BC=3,求AB、AC.