题目内容
2.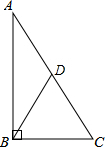 如图,在直角三角形ABC中,两直角边边长分别为6cm和8cm,则连接顶点B与斜边中点D的线段长为( )
如图,在直角三角形ABC中,两直角边边长分别为6cm和8cm,则连接顶点B与斜边中点D的线段长为( )| A. | 10cm | B. | 3cm | C. | 4cm | D. | 5cm |
分析 根据勾股定理求出斜边AC,再根据直角三角形斜边上的中线性质求出即可.
解答 解:由勾股定理得:AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{8}^{2}+{6}^{2}}$=10(cm),
∵BD是直角三角形ABC斜边上的中线,
∴BD=$\frac{1}{2}$AC=5cm,
故选D.
点评 本题考查了直角三角形斜边上的中线性质和勾股定理的应用,能得出BD=$\frac{1}{2}$AC是解此题的关键,注意:直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
相关题目
10. 实数a,b在数轴上的位置如图所示,下列各式不成立的是( )
实数a,b在数轴上的位置如图所示,下列各式不成立的是( )
 实数a,b在数轴上的位置如图所示,下列各式不成立的是( )
实数a,b在数轴上的位置如图所示,下列各式不成立的是( )| A. | $\sqrt{(a-b)^{2}}$=b-a | B. | $\sqrt{a+b}$<$\sqrt{b}$ | C. | |a+$\sqrt{5}$|=a+$\sqrt{5}$ | D. | |b-$\sqrt{5}$|=b-$\sqrt{5}$ |
17.α,β是方程x2+2x-5=0的两个实数根,则αβ的值为( )
| A. | 5 | B. | -5 | C. | 2 | D. | -2 |
14.将一个平行四边形的纸片折一次,使得折痕平分这个平行四边形的面积,则这样的折纸方法共有( )
| A. | 1种 | B. | 2种 | C. | 3种 | D. | 无数种 |
11.40°角的余角是( )
| A. | 50° | B. | 60° | C. | 120° | D. | 140° |
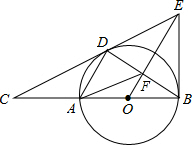 如图,点D是半径为5的⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD,CA=8,过点B作⊙O的切线BE交直线CD于点E,连接AD、BD、OE的交点是F,连接AF.
如图,点D是半径为5的⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD,CA=8,过点B作⊙O的切线BE交直线CD于点E,连接AD、BD、OE的交点是F,连接AF. 在Rt△ABC中,已知∠C=90°,∠A=30°,BC=3,求AB、AC.
在Rt△ABC中,已知∠C=90°,∠A=30°,BC=3,求AB、AC.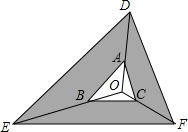 如图,点O是△ABC内一点、分别连接OA、OB、OC并延长到点D、E、F,使AD=2OA,BE=2OB,CF=2OC,连接DE,EF,FD.若△ABC的面积是3,则阴影部分的面积是( )
如图,点O是△ABC内一点、分别连接OA、OB、OC并延长到点D、E、F,使AD=2OA,BE=2OB,CF=2OC,连接DE,EF,FD.若△ABC的面积是3,则阴影部分的面积是( )