题目内容
10.若(a+3)2+(3b-1)2=0,则a2003•b2004=$-\frac{1}{3}$.分析 根据非负数的性质列出算式,求出a、b的值,根据积的乘方法则计算即可.
解答 解:由题意得,a+3=0,3b-1=0,
解得,a=-3,b=$\frac{1}{3}$,
则a2003•b2004=则a2003•b2003•b=(ab)2003•b=$-\frac{1}{3}$,
故答案为:-$\frac{1}{3}$.
点评 本题考查的是非负数的性质,掌握当几个非负数相加和为0时,则其中的每一项都必须等于0是解题的关键.

练习册系列答案
相关题目
1.下列两个多项式相乘,可用平方差公式的是( )
| A. | (2a-3b)(3b-2a) | B. | (-2a+3b)(2a+3b) | C. | (-2a+3b)(2a-3b) | D. | (2a+3b)(-2a-3b) |
5.世界卫生组织宣布:冠状病毒的一个变种足以引起非典型的病原体,某种冠状病毒的直径约为0.00000012米,则这种冠状病毒的直径用科学记数法表示为( )
| A. | 120×10-9米 | B. | 1.2×10-7米 | C. | 1.20×10-6米 | D. | 12×10-4米 |
19.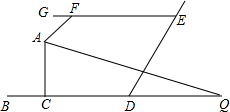 如图,BD∥GE,AQ平分∠FAC,交BD于Q,∠GFA=50°,∠Q=25°,则∠ACB的度数( )
如图,BD∥GE,AQ平分∠FAC,交BD于Q,∠GFA=50°,∠Q=25°,则∠ACB的度数( )
 如图,BD∥GE,AQ平分∠FAC,交BD于Q,∠GFA=50°,∠Q=25°,则∠ACB的度数( )
如图,BD∥GE,AQ平分∠FAC,交BD于Q,∠GFA=50°,∠Q=25°,则∠ACB的度数( )| A. | 90° | B. | 95° | C. | 100° | D. | 105° |
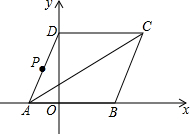 如图所示,菱形ABCD的顶点A、B在x轴上,点A在点B的左侧,点D在y轴的正半轴上,∠BAD=60°.点A的坐标为(-2,0).
如图所示,菱形ABCD的顶点A、B在x轴上,点A在点B的左侧,点D在y轴的正半轴上,∠BAD=60°.点A的坐标为(-2,0).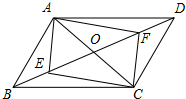 如图,在?ABCD中,AC与BD交于点O,点E,F都在BD上,BE=DF.
如图,在?ABCD中,AC与BD交于点O,点E,F都在BD上,BE=DF.