Question

12．在直角坐标系中，已知线段AB，点A的坐标为（1，-2），点B的坐标为（3，0），如图1所示．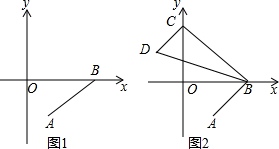

（1）平移线段AB到线段CD，使点A的对应点为D，点B的对应点为C，若点C的坐标为（-2，4），求点D的坐标；
（2）平移线段AB到线段CD，使点C在y轴的正半轴上，点D在第二象限内，连接BC，BD，如图2所示．若S_△BCD=7（S_△BCD表示三角形BCD的面积），求点C、D的坐标．
（3）在（2）的条件下，在y轴上是否存在一点P，使$\frac{{S}_{△PCD}}{{S}_{△BCD}}$=$\frac{2}{3}$（S_△PCD表示三角形PCD的面积）？若存在，求出点P的坐标；若不存在，请说明理由．

Answer 1

分析 （1）利用平移得性质确定出平移得单位和方向；
（2）根据平移得性质，设出平移单位，根据S_△BCD=7（S_△BCD建立方程求解，即可，
（3）设出点P的坐标，表示出PC用$\frac{{S}_{△PCD}}{{S}_{△BCD}}$=$\frac{2}{3}$，建立方程求解即可．

解答 解：（1）∵B（3，0）平移后的对应点C（-2，4），
∴设3+a=-2，0+b=4，
∴a=-5，b=4，
即：点B向左平移5个单位，再向上平移4个单位得到点C（-2，4），
∴A点平移后的对应点D（-4，2），
（2）∵点C在y轴上，点D在第二象限，
∴线段AB向左平移3个单位，再向上平移（2+y）个单位，符合题意，
∴C（0，2+y），D（-2，y），
连接OD，
S_△BCD=S_△BOC+S_△COD-S_△BOD
=$\frac{1}{2}$OB×OC+$\frac{1}{2}$OC×2-$\frac{1}{2}$OB×y=7，
∴y=2，
∴C（0，4）．D（-2，2）；
（3）设点P（0，m），
∴PC=|4-m|，
∵$\frac{{S}_{△PCD}}{{S}_{△BCD}}$=$\frac{2}{3}$，
∴$\frac{1}{2}$|4-m|×2=$\frac{2}{3}$×7，
∴|4-m|=$\frac{14}{3}$，
∴m=-$\frac{2}{3}$或m=$\frac{26}{3}$，
∴存在点P，其坐标为（0，-$\frac{2}{3}$）或（0，$\frac{26}{3}$）．

点评 此题是几何变换综合题，主要考查了平移得性质，解本题的关键是平移性质的灵活运用，用面积关系建立方程．