题目内容
11.解方程:$\frac{x}{x-3}+\frac{2-x}{3-x}=1$.分析 两边乘(x-3)转化为整式方程即可,注意必须检验.
解答 解:两边乘(x-3)得到x-(2-x)=x-3,
x-2+x=x-3,
x=-1,
检验:当x=-1时,x-3≠0,
故x=-1是分式方程的根.
点评 本题考查分式方程的解,熟练掌握解分式方程的步骤是解题的关键,注意解分式方程必须检验,属于基础题,中考常考题型.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
1.下列两个多项式相乘,可用平方差公式的是( )
| A. | (2a-3b)(3b-2a) | B. | (-2a+3b)(2a+3b) | C. | (-2a+3b)(2a-3b) | D. | (2a+3b)(-2a-3b) |
19.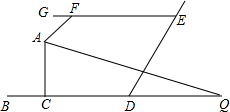 如图,BD∥GE,AQ平分∠FAC,交BD于Q,∠GFA=50°,∠Q=25°,则∠ACB的度数( )
如图,BD∥GE,AQ平分∠FAC,交BD于Q,∠GFA=50°,∠Q=25°,则∠ACB的度数( )
 如图,BD∥GE,AQ平分∠FAC,交BD于Q,∠GFA=50°,∠Q=25°,则∠ACB的度数( )
如图,BD∥GE,AQ平分∠FAC,交BD于Q,∠GFA=50°,∠Q=25°,则∠ACB的度数( )| A. | 90° | B. | 95° | C. | 100° | D. | 105° |
6.下列说法正确的是( )
| A. | 有公共顶点且又相等的角是对顶角 | |
| B. | 同旁内角相等,两直线平行 | |
| C. | 过直线外一点有且只有一条直线与已知直线平行 | |
| D. | 过一点有且只有一条直线与已知直线垂直 |
3.下列运算结果正确的是( )
| A. | 3x2+4x2=7x4 | B. | x3×x5=x15 | C. | x4÷x=x3 | D. | (x5)2=x7 |
1. 如图,数轴上表示1、$\sqrt{3}$的对应点分别为点A、点B.若点A是BC的中点,则点C所表示的数为( )
如图,数轴上表示1、$\sqrt{3}$的对应点分别为点A、点B.若点A是BC的中点,则点C所表示的数为( )
 如图,数轴上表示1、$\sqrt{3}$的对应点分别为点A、点B.若点A是BC的中点,则点C所表示的数为( )
如图,数轴上表示1、$\sqrt{3}$的对应点分别为点A、点B.若点A是BC的中点,则点C所表示的数为( )| A. | $\sqrt{3}-1$ | B. | 1-$\sqrt{3}$ | C. | $\sqrt{3}-2$ | D. | 2-$\sqrt{3}$ |
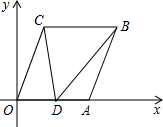 如图,在直角坐标系xOy中,已知A(6,0),B(8,6),将线段OA平移至CB,点D在x轴正半轴上(不与点A重合),连接OC,AB,CD,BD.
如图,在直角坐标系xOy中,已知A(6,0),B(8,6),将线段OA平移至CB,点D在x轴正半轴上(不与点A重合),连接OC,AB,CD,BD.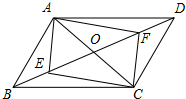 如图,在?ABCD中,AC与BD交于点O,点E,F都在BD上,BE=DF.
如图,在?ABCD中,AC与BD交于点O,点E,F都在BD上,BE=DF.