题目内容
20．
如图，?ABCD的对角线AC与BD相交于点O，AB⊥AC，若AB=4，AC=6，则BD=10．
分析 利用平行四边形的性质和勾股定理易求BO的长，进而可求出BD的长．
解答 解：∵?ABCD的对角线AC与BD相交于点O，
∴BO=DO，AO=CO，
∵AB⊥AC，AB=4，AC=6，
∴BO=$\sqrt{{3}^{2}+{4}^{2}}$=5，
∴BD=2BO=10，
故答案为：10．
点评 本题考查了平行四边形的性质以及勾股定理的运用，是中考常见题型，比较简单．
练习册系列答案
相关题目
8．解分式方程$\frac{2}{x+1}+\frac{3}{x-1}=\frac{6}{{{x^2}-1}}$，分以下四步，其中，错误的一步是（ ）
| A． | 方程两边分式的最简公分母是（x-1）（x+1） | |
| B． | 方程两边都乘以（x-1）（x+1），得整式方程2（x-1）+3（x+1）=6 | |
| C． | 解这个整式方程，得x=1 | |
| D． | 原方程的解为x=1 |
如图，正方形ABCD的边长为4，P为CD边上一点（与点D不重合）．设DP=x，△APD的面积y关于x的函数关系式．
5．
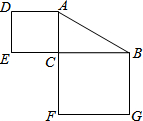如图，在Rt△ABC中，∠C=90°，若AB=15，则正方形ADEC和正方形BCFG的面积和为（ ）
如图，在Rt△ABC中，∠C=90°，若AB=15，则正方形ADEC和正方形BCFG的面积和为（ ）| A． | 225 | B． | 200 | C． | 250 | D． | 150 |
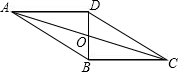如图，四边形ABCD是平行四边形，对角线AC、BD相交于点O，BD⊥AD，AD=6，AB=10，求DC，BC及平行四边形ABCD的面积？