题目内容
10.如图①,底面积为30cm2的空圆柱形容器内水平放置着由两个实心圆柱组成的“几何体”,现向容器匀速注水,注满为止,在注水过程中,水面高度h(cm)与注水时间t(s)之间的关系如图②所示.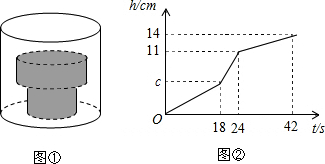
试根据图中提供的信息,解答下列问题:
(1)圆柱形容器的高为14cm,匀速注水流速度为5cm2/s;
(2)若“几何体”的下方圆柱的底面积为15cm2,则图中②中a的值为6cm;
(3)在(2)的条件下,求“几何体”上方圆柱的高和底面积.
(友情提醒:圆柱的体积=底面积×高)
分析 (1)根据图象,分三个部分:满过“几何体”下方圆柱需18s,满过“几何体”上方圆柱需24s-18s=6s,注满“几何体”上面的空圆柱形容器需42s-24s=18s,再设匀速注水的水流速度为xcm3/s,根据圆柱的体积公式列方程,再解方程;
(2)根据圆柱的体积公式得a•(30-15)=18•5,解得a=6;
(3)根据圆柱的体积公式得a•(30-15)=18•5,解得a=6,于是得到“几何体”上方圆柱的高为5cm,设“几何体”上方圆柱的底面积为Scm2,根据圆柱的体积公式得5•(30-S)=5•(24-18),再解方程即可.
解答 解:(1)根据函数图象得到圆柱形容器的高为14cm,两个实心圆柱组成的“几何体”的高度为11cm,
水从刚满过由两个实心圆柱组成的“几何体”到注满用了42s-24s=18s,这段高度为14-11=3cm,
设匀速注水的水流速度为xcm3/s,则18•x=30•3,解得x=5,
即匀速注水的水流速度为5cm3/s;
故答案为:14,5;
(2)“几何体”下方圆柱的高为a,则a•(30-15)=18•5,解得a=6,故答案为:6;
(3)由a=6可得,所以“几何体”上方圆柱的高为11cm-6cm=5cm,
设“几何体”上方圆柱的底面积为Scm2,根据题意得5•(30-S)=5•(24-18),解得S=24,
即“几何体”上方圆柱的底面积为24cm2.
点评 本题考查了一次函数的应用:把分段函数图象中自变量与对应的函数值转化为实际问题中的数量关系,然后运用方程的思想解决实际问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.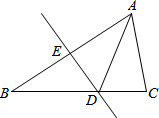 如图,DE为AB边的垂直平分线,若△ACD的周长为7cm,若△ABC的周长为12cm,则AB长为( )
如图,DE为AB边的垂直平分线,若△ACD的周长为7cm,若△ABC的周长为12cm,则AB长为( )
 如图,DE为AB边的垂直平分线,若△ACD的周长为7cm,若△ABC的周长为12cm,则AB长为( )
如图,DE为AB边的垂直平分线,若△ACD的周长为7cm,若△ABC的周长为12cm,则AB长为( )| A. | 5cm | B. | 6cm | C. | 7cm | D. | 8cm |
 如图,?ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BD=10.
如图,?ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BD=10. 如图,在正方形ABCD的对角线上取点E,使得∠BAE=15°,连接AE,CE,延长CE到F,连接BF,使得BC=BF.若AB=1,则下列结论:①AE=CE;②F到BC的距离为$\frac{1}{2}$;③∠AEF=60°;④图中只有三对三角形全等;⑤DE=$\frac{\sqrt{6}+\sqrt{2}}{2}$.其中正确的个数是( )
如图,在正方形ABCD的对角线上取点E,使得∠BAE=15°,连接AE,CE,延长CE到F,连接BF,使得BC=BF.若AB=1,则下列结论:①AE=CE;②F到BC的距离为$\frac{1}{2}$;③∠AEF=60°;④图中只有三对三角形全等;⑤DE=$\frac{\sqrt{6}+\sqrt{2}}{2}$.其中正确的个数是( )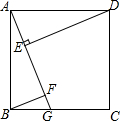 已知:在正方形ABCD中,点G是BC边上的任意一点,DE⊥AG于点E,BF∥DE,交AG于点F.求证:AF=BF+EF.
已知:在正方形ABCD中,点G是BC边上的任意一点,DE⊥AG于点E,BF∥DE,交AG于点F.求证:AF=BF+EF.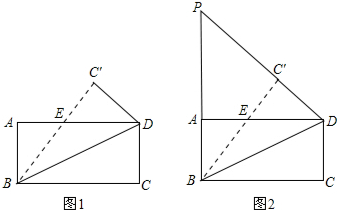
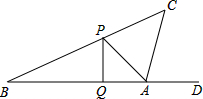 2015年 4月18日潍坊国际风筝节拉开了帷幕,这天小敏同学正在公园广场上放风筝,如图风筝从A处起飞,几分钟后便飞达C处,此时,在AQ延长线上B处的小亮同学,发现自己的位置与风筝和广场边旗杆PQ的顶点P在同一直线上.
2015年 4月18日潍坊国际风筝节拉开了帷幕,这天小敏同学正在公园广场上放风筝,如图风筝从A处起飞,几分钟后便飞达C处,此时,在AQ延长线上B处的小亮同学,发现自己的位置与风筝和广场边旗杆PQ的顶点P在同一直线上.