题目内容
5.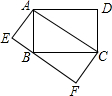 如图,矩形ABCD和矩形AEFC的面积分别为S1,S2,当点B在EF边上时,则S1与S2之间的数量关系为:S1=S2.
如图,矩形ABCD和矩形AEFC的面积分别为S1,S2,当点B在EF边上时,则S1与S2之间的数量关系为:S1=S2.
分析 由于矩形ABCD的面积等于2个△ABC的面积,而△ABC的面积又等于矩形AEFC的一半,所以可得两个矩形的面积关系.
解答 解:∵矩形ABCD的面积S1=2S△ABC,S△ABC=$\frac{1}{2}$S矩形AEFC,
∴S1=S2.
故答案为:S1=S2.
点评 本题主要考查了矩形的性质及面积的计算,能够熟练运用矩形的性质进行一些面积的计算问题.

练习册系列答案
相关题目
16.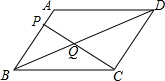 如图,在平行四边形ABCD中,点P在AB上,连接CP,交BD于点Q,当AP=$\frac{1}{4}$AB时,△BQC的面积为3,则平行四边形ABCD的面积为( )
如图,在平行四边形ABCD中,点P在AB上,连接CP,交BD于点Q,当AP=$\frac{1}{4}$AB时,△BQC的面积为3,则平行四边形ABCD的面积为( )
 如图,在平行四边形ABCD中,点P在AB上,连接CP,交BD于点Q,当AP=$\frac{1}{4}$AB时,△BQC的面积为3,则平行四边形ABCD的面积为( )
如图,在平行四边形ABCD中,点P在AB上,连接CP,交BD于点Q,当AP=$\frac{1}{4}$AB时,△BQC的面积为3,则平行四边形ABCD的面积为( )| A. | 9 | B. | 11 | C. | 12 | D. | 14 |
10. 如图,E是?ABCD内任一点,若S?ABCD=8,则阴影部分的面积是( )
如图,E是?ABCD内任一点,若S?ABCD=8,则阴影部分的面积是( )
 如图,E是?ABCD内任一点,若S?ABCD=8,则阴影部分的面积是( )
如图,E是?ABCD内任一点,若S?ABCD=8,则阴影部分的面积是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
17.若反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点A(-2,1),则当x<-1时,函数值y的取值范围是( )
| A. | y>2 | B. | -2<y<0 | C. | y>-2 | D. | 0<y<2 |
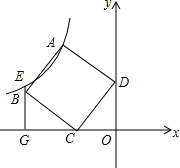 如图,在平面直角坐标系中,四边形ABCD为正方形,点C(-3,0),D(0,4),过B点作x轴的垂线交过A点的反比例函数图象于E点,交x轴于G点.
如图,在平面直角坐标系中,四边形ABCD为正方形,点C(-3,0),D(0,4),过B点作x轴的垂线交过A点的反比例函数图象于E点,交x轴于G点.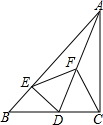 如图,在Rt△ABC中,∠ACB=90°,D是边BC上一点,DE⊥AB于点E,点F是线段AD上一点,连接EF,CF.
如图,在Rt△ABC中,∠ACB=90°,D是边BC上一点,DE⊥AB于点E,点F是线段AD上一点,连接EF,CF.
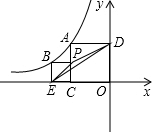 如图,A,B(点B在点A左边)分别是反比例函数y=$\frac{k}{x}$(x<0)图象上的两,过点A作两坐标轴的垂线,得到正方形ACOD,过点B作x轴和AC的垂线,得到正方形BECP.连接EP和DE,已知△PED的面积为2,则k的值为-6-2$\sqrt{5}$.
如图,A,B(点B在点A左边)分别是反比例函数y=$\frac{k}{x}$(x<0)图象上的两,过点A作两坐标轴的垂线,得到正方形ACOD,过点B作x轴和AC的垂线,得到正方形BECP.连接EP和DE,已知△PED的面积为2,则k的值为-6-2$\sqrt{5}$.