题目内容
15.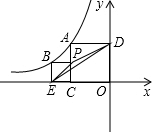 如图,A,B(点B在点A左边)分别是反比例函数y=$\frac{k}{x}$(x<0)图象上的两,过点A作两坐标轴的垂线,得到正方形ACOD,过点B作x轴和AC的垂线,得到正方形BECP.连接EP和DE,已知△PED的面积为2,则k的值为-6-2$\sqrt{5}$.
如图,A,B(点B在点A左边)分别是反比例函数y=$\frac{k}{x}$(x<0)图象上的两,过点A作两坐标轴的垂线,得到正方形ACOD,过点B作x轴和AC的垂线,得到正方形BECP.连接EP和DE,已知△PED的面积为2,则k的值为-6-2$\sqrt{5}$.
分析 根据题意设出点A、B的坐标,然后根据点A、B都在反比例函数的图象上,可得两点坐标的关系,然后根据△PED的面积为2,可以得到k的值,本题得以解决.
解答 解:解法一:设点A的坐标是(a,-a),点B的坐标是(b,c),
由题意可得,$\left\{\begin{array}{l}{a•(-a)=bc}\\{c=a-b}\\{{a}^{2}+{c}^{2}-\frac{(-b)•(-a)}{2}-\frac{{c}^{2}}{2}-\frac{(-a-c)(-a)}{2}=2}\end{array}\right.$
解得c=2,b=$-3±\sqrt{5}$,
∴a=$-1-\sqrt{5}$或a=$-1+\sqrt{5}$(舍去),
∴a•(-a)=$(-1-\sqrt{5})(1+\sqrt{5})$=$-6-2\sqrt{5}$.
故答案为:$-6-2\sqrt{5}$.
解法二:设点A的坐标是(a,-a),点B的坐标是(-a-b,b),AC与ED交于点F,
由题意可得,△ECP∽△EOD,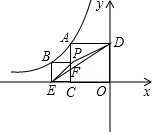
则$\frac{CF}{OD}=\frac{EC}{EO}$,即$\frac{CF}{a}=\frac{b}{b+a}$,
得CF=$\frac{ab}{a+b}$,
∵△PED的面积为2,
∴$\frac{(a+b)(b-\frac{ab}{a+b})}{2}$=2,
解得,b=2,
∵(-a)•a=(-a-b)b,
解得,a=$-1-\sqrt{5}$或a=$-1+\sqrt{5}$(舍去),
∴a•(-a)=$(-1-\sqrt{5})(1+\sqrt{5})$=$-6-2\sqrt{5}$.
故答案为:$-6-2\sqrt{5}$.
点评 本题考查反比例函数系数k的几何意义,解题的关键是明确题意,列出相应的关系式,求出相应的k的值.

 阅读快车系列答案
阅读快车系列答案 如图,菱形ABCD的对角线BD长为4$\sqrt{3}$cm,高AE长为2$\sqrt{3}$cm,则菱形ABCD的周长为( )
如图,菱形ABCD的对角线BD长为4$\sqrt{3}$cm,高AE长为2$\sqrt{3}$cm,则菱形ABCD的周长为( )| A. | 20cm | B. | 16cm | C. | 12cm | D. | 8cm |
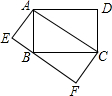 如图,矩形ABCD和矩形AEFC的面积分别为S1,S2,当点B在EF边上时,则S1与S2之间的数量关系为:S1=S2.
如图,矩形ABCD和矩形AEFC的面积分别为S1,S2,当点B在EF边上时,则S1与S2之间的数量关系为:S1=S2.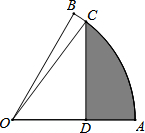 如图,扇形OAB中,∠AOB=60°,扇形半径为3,点C在AB上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为$\frac{9}{8}π-\frac{9}{4}$.
如图,扇形OAB中,∠AOB=60°,扇形半径为3,点C在AB上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为$\frac{9}{8}π-\frac{9}{4}$.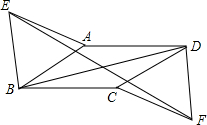 如图,在?ABCD中,分别以AB、CD为边向外作等边△ABE和等边△CDF,
如图,在?ABCD中,分别以AB、CD为边向外作等边△ABE和等边△CDF, 如图,在矩形ABCD中,∠BOC=120°,则∠BAC=60°.
如图,在矩形ABCD中,∠BOC=120°,则∠BAC=60°.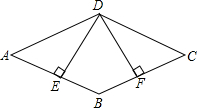 如图,四边形ABCD是平行四边形,DE⊥BC,垂足分别是E,F,且DE=FD.
如图,四边形ABCD是平行四边形,DE⊥BC,垂足分别是E,F,且DE=FD.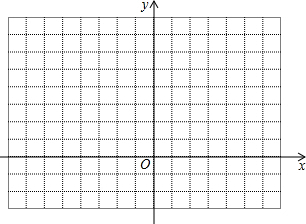 (1)在平面直角坐标系中,描出下列3个点:A (-1,0),B (3,-1),C (4,3);顺次连接A,B,C,组成△ABC.
(1)在平面直角坐标系中,描出下列3个点:A (-1,0),B (3,-1),C (4,3);顺次连接A,B,C,组成△ABC.