题目内容
13．已知：P为?ABCD内一点，S?ABCD=100，则S△PAB+S△PCD=50．分析 过P点作一条平行AB的直线EF，可得S△PAB的面积是平行四边形ABFE的一半，S△PCD是平行四边形EFCD的一半，继而可得出S△PAB+S△PCD=S?ABCD，即可得出结果．
解答 证明：过P点作EF∥AB交AD于E，BC于F，如图所示：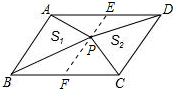
∵AB∥CD，
∴EF∥CD，
则S△PAB=$\frac{1}{2}$S?ABEF，S△PCD=$\frac{1}{2}$S?EFDC，
∵S?ABEF+S?EFDC=S?ABCD=100，
∴S△PAB+S△PCD=$\frac{1}{2}$×100=50；
故答案为：50．
点评 本题考查了平行四边形的性质、三角形面积与平行四边形的面积关系；熟练掌握平行四边形的性质，证出S△PAB+S△PCD=S?ABCD是解决问题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
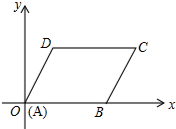在平面直角坐标系中，?ABCD的顶点A，B，D的坐标分别是（0，0），（5，0），（2，3）．
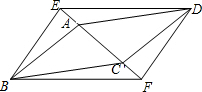如图，?ABCD和?EBFD的顶点A，C，E，F在同一条直线上，求证：AE=CF．
如图，菱形ABCD与菱形ECGF中，点D在CE上，点B、C、G在一条直线上，AB=2，CG=4，∠ABC=60°，连接BD，DF，BF，则图中阴影部分的周长为$\sqrt{3}$．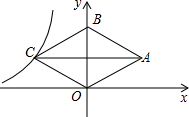
如图，在平面直角坐标系中，菱形OABC的顶点B在y轴正半轴上，菱形的两条对角线的长分别是6和4，函数y=$\frac{k}{x}（x＜0）$的图象经过点C，则k的值为-6．
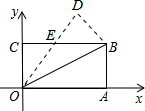如图，在矩形OABC中，OA=8，OC=4，沿对角线OB折叠后，点A与点D重合，OD与BC交于点E，试求点D的坐标．
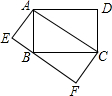如图，矩形ABCD和矩形AEFC的面积分别为S1，S2，当点B在EF边上时，则S1与S2之间的数量关系为：S1=S2．
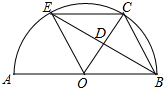如图，AB是半圆O的直径，点C是半圆O上一点，∠COB=60°，点D是OC的中点，连接BD，BD的延长线交半圆O于点E，连接OE，EC，BC．