题目内容
14.如图,在平面直角坐标系中,点O为坐标原点,抛物线y=-$\frac{3}{16}a{x}^{2}$+$\frac{5}{8}ax$+3a(a≠0)与x轴交于点A和点B(点A在点B的左侧),与y轴的正半轴交于点C,且OB=OC.(1)求a的值;
(2)点D为OB中点,点E为OC中点,点F在y轴的负半轴上,点G在线段FD的延长线上,连接GE、ED,若FD=DG,且S△GED=$\frac{27}{2}$,求点G的坐标;
(3)在(2)的条件下,点P在线段OB上,点Q在线段OC的延长线上,且CQ=BP.连接PQ和BC交于点M,连接GM并延长GM交抛物线于点N,连接QN、GP和GB,若∠QPG-∠NQO=∠NQP-∠PGB时,求线段NQ的长.
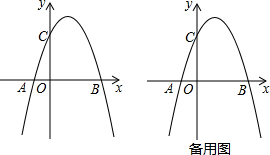
分析 (1)令y=0可求得点A、B的坐标,将x=0代入抛物线的解析式得求得点C(0,3a),然后根据OB=0C可求得a的值,从而得到抛物线的解析式;
(2)连接GB.首先依据SAS证明△ODF≌△GDB,从而得到BG=OF,接下来依据S△GED=$\frac{27}{2}$可求得EF的长,从而得到BG的长,故此可得到点G的坐标;
(3)过点P作PT∥y轴,交BC与点T,过点N作NR⊥y轴,垂足为R.先证明TP=PB=CQ,然后依据ASA证明△PTM≌△QCM,于是可得到PM=QM,然后再证明△NMQ≌△GMP,于是得到NQ=GP,然后再△QNR≌△GPB,从而可求得NR=OR,设N(t,-$\frac{3}{8}$t2+$\frac{5}{4}$t+6),由NR=OR列出关于t的方程,从而可求得NR的值,最后在Rt△NRQ中,依据勾股定理可求得QN的值.
解答 解:(1)将y=0代入得:-$\frac{3}{16}a{x}^{2}$+$\frac{5}{8}ax$+3a=0,
∵a≠0,
∴$-\frac{3}{16}$x2+$\frac{5}{8}$x+3=0.
解得:x1=-$\frac{8}{3}$,x2=6.
∴A(-$\frac{8}{3}$,0)、B(6,0).
∴0B=6.
∵将x=0代入抛物线的解析式得:y=3a,
∴C(0,3a).
∴OC=3a.
∵OB=0C,
∴3a=6.
解得:a=2.
∴抛物线的解析式为y=-$\frac{3}{8}$x2+$\frac{5}{4}$x+6.
(2)如图1所示:连接GB.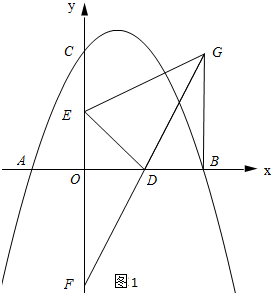
∵E、D分别是OC、0B的中点,
∴OE=3,OD=BD.
在△ODF和△GDB中,
$\left\{\begin{array}{l}{OD=BD}\\{∠ODF=∠BDG}\\{DF=DG}\end{array}\right.$,
∴△ODF≌△GDB.
∴BG=OF,∠GBD=∠FOD=90°.
∵S△EDG=S△EFG-S△EFD,
∴$\frac{1}{2}$EF•OB-$\frac{1}{2}$EF•OD=$\frac{27}{2}$,即3EF-$\frac{3}{2}$EF=$\frac{27}{2}$,解得:EF=9.
∴OF=EF-OE=9-3=6.
∴BG=6.
∴G(6,6).
(3)如图2所示:过点P作PT∥y轴,交BC与点T,过点N作NR⊥y轴,垂足为R.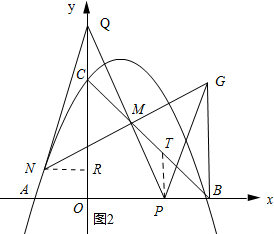
∵TP∥OQ,
∴∠MPT=∠MQC,∠PTM=∠QCM,
∵OB=0C=6,
∴∠OCB=∠OBC=45°,
∴∠PBT=∠PTB=45°,
∴PT=PB=CQ,
在△PTM和△QCM中,
$\left\{\begin{array}{l}{∠MPT=∠MQC}\\{PT=CQ}\\{∠PTM=∠QCM}\end{array}\right.$,
∴△PTM≌△QCM,
∴PM=QM,
∵GB⊥x轴,
∴BG∥y轴∥PT,
∴∠BGP=∠TPG.
∵∠QPG-∠NQO=∠NQP-∠PGB,
∴∠QPT+∠TPG-∠NQO=∠NQO+∠OQP-∠PCB,
∵∠QPT=∠OQP,∠TPG=∠PGB,
∴2∠TPG=2∠NQO,
∴∠TPG=∠NQO,
∴∠NQP=∠GPQ,
在△NMQ和△GMP中,
$\left\{\begin{array}{l}{∠NQP=∠GPQ}\\{∠NMQ=∠GMP}\\{MQ=MP}\end{array}\right.$,
∴△NMQ≌△GMP.
∴NQ=GP.
在Rt△QNR和Rt△GPB中,
$\left\{\begin{array}{l}{∠BGP=∠NQO}\\{∠QRN=∠GBP=90°}\\{NQ=GP}\end{array}\right.$,
∴△QNR≌△GPB.
∴QM=BG=6,NR=PB=CQ.
设N(t,-$\frac{3}{8}$t2+$\frac{5}{4}$t+6).
∵QO=QC+C0=QR+RO,
∴QC=RO,
∴NR=RO,
∴-t=-$\frac{3}{8}$t2+$\frac{5}{4}$t+6,解得:t1=-2,t2=8(舍去).
∴NR=2.
在Rt△NRQ中,NQ=$\sqrt{N{R}^{2}+Q{R}^{2}}$=2$\sqrt{10}$.
∴线段NQ的长为2$\sqrt{10}$.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用待定系数法求二次函数的解析式、二次函数的性质、勾股定理、全等三角形的性质和判定,函数图象与坐标轴的交点,证得△PTM≌△QCM、△NMQ≌△GMP、△QNR≌△GPB,从而可求得NR=OR,然后依据NR=OR列出关于t的方程是解题的关键.

 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案 如图,菱形ABCD的对角线BD长为4$\sqrt{3}$cm,高AE长为2$\sqrt{3}$cm,则菱形ABCD的周长为( )
如图,菱形ABCD的对角线BD长为4$\sqrt{3}$cm,高AE长为2$\sqrt{3}$cm,则菱形ABCD的周长为( )| A. | 20cm | B. | 16cm | C. | 12cm | D. | 8cm |
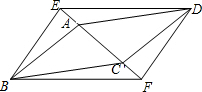 如图,?ABCD和?EBFD的顶点A,C,E,F在同一条直线上,求证:AE=CF.
如图,?ABCD和?EBFD的顶点A,C,E,F在同一条直线上,求证:AE=CF.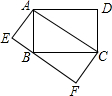 如图,矩形ABCD和矩形AEFC的面积分别为S1,S2,当点B在EF边上时,则S1与S2之间的数量关系为:S1=S2.
如图,矩形ABCD和矩形AEFC的面积分别为S1,S2,当点B在EF边上时,则S1与S2之间的数量关系为:S1=S2.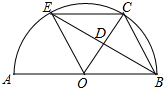 如图,AB是半圆O的直径,点C是半圆O上一点,∠COB=60°,点D是OC的中点,连接BD,BD的延长线交半圆O于点E,连接OE,EC,BC.
如图,AB是半圆O的直径,点C是半圆O上一点,∠COB=60°,点D是OC的中点,连接BD,BD的延长线交半圆O于点E,连接OE,EC,BC.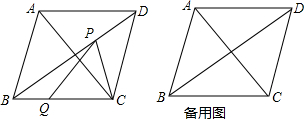 如图,菱形ABCD中,∠ABC<90°,P为该菱形对角线BD上一动点,Q为BC边上一动点,若AC=30,PC+PQ的最小值为24,求菱形ABCD的边长(要求在备用图中画出必要的图形)
如图,菱形ABCD中,∠ABC<90°,P为该菱形对角线BD上一动点,Q为BC边上一动点,若AC=30,PC+PQ的最小值为24,求菱形ABCD的边长(要求在备用图中画出必要的图形)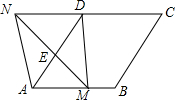 如图,在菱形ABCD中,AB=2,∠DAB=60°,点E时AD边的中点,点M时AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.
如图,在菱形ABCD中,AB=2,∠DAB=60°,点E时AD边的中点,点M时AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.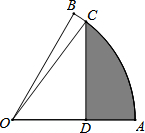 如图,扇形OAB中,∠AOB=60°,扇形半径为3,点C在AB上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为$\frac{9}{8}π-\frac{9}{4}$.
如图,扇形OAB中,∠AOB=60°,扇形半径为3,点C在AB上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为$\frac{9}{8}π-\frac{9}{4}$.