题目内容
2．
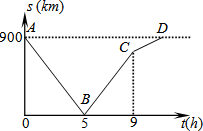一列快车由甲地开往乙地，一列慢车由乙地开往甲地，两车同时出发，沿同一条道路匀速行驶．设行驶时间为t（h），两车之间的距离为s（km），图中折线A-B-C-D表示s与t之间的函数关系．（1）甲、乙两地相距900km，两车出发后5h相遇；
（2）通过计算说明，当快车到达乙地时，慢车还要多少时间才能到达甲地？
分析 （1）由图可知，甲、乙两地的路程为900千米，当t=5时，s=0，所以甲、乙两车相遇的时间为4小时；
（2）由图可知，快车单独行使9小时行完全程，所以快车速度：900÷9=100（km/h），慢车速度 900÷5-100=80（km/h），所以当快车到达乙地时，慢车还要900÷80-9=$\frac{9}{4}$（h）才能到达甲地．
解答 解：（1）由图可知，甲、乙两地的路程为900千米，当t=5时，s=0，
所以甲、乙两车相遇的时间为4小时；
故答案为：900，5．
（2）由图可知，快车单独行使9小时行完全程，
快车速度：900÷9=100（km/h），
慢车速度 900÷5-100=80（km/h），
900÷80-9=$\frac{9}{4}$（h）．
答：当快车到达乙地时，慢车还要$\frac{9}{4}$小时才能到达甲地．
点评 此题主要考查了函数图象的应用，根据题意得出快慢车行完全程所需时间是解题关键．
练习册系列答案
相关题目
13．问题情境
初次见面，通常以握手示礼，适当的握手时间与力度，会让人有股舒服亲切的感受．9月1日开学时，老师为了让全班新同学互相认识，请班上41位同学彼此握手为礼，并同时彼此介绍自己．在一阵喧哗后，同学完成工作．老师提出一个问题：“谁知道，刚才全班同学总共握手几次？”小聪同学举手抢答说820次，他说的对不对？
探索研究
其实要解决握手问题，可以作以下的分析：假若两点代表两个人，连接两点的线段数目，就表示握手的次数． 我们可以作一个由点和线段组成的图来分析一下
因此，n个人握手总次为P=1+2+3…+（n+1）=$\frac{n（n-1）}{2}$
解决问题
班上41位同学彼此握手为礼，他们共握手多少次？小聪同学说的对不对？
问题拓展
请你用仿照上述方法来研究平面内n条直线最多有多少个交点？请你完成下表：
因此，平面内n条直线最多交点的个数为$\frac{{n（{n-1}）}}{2}$．
初次见面，通常以握手示礼，适当的握手时间与力度，会让人有股舒服亲切的感受．9月1日开学时，老师为了让全班新同学互相认识，请班上41位同学彼此握手为礼，并同时彼此介绍自己．在一阵喧哗后，同学完成工作．老师提出一个问题：“谁知道，刚才全班同学总共握手几次？”小聪同学举手抢答说820次，他说的对不对？
探索研究
其实要解决握手问题，可以作以下的分析：假若两点代表两个人，连接两点的线段数目，就表示握手的次数． 我们可以作一个由点和线段组成的图来分析一下
| 握手图标 | 握手人数 | 握手次数 |
 | 2 | 1 |
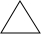 | 3 | 3=1+2 |
 | 4 | 6=1+2+3 |
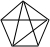 | 5 | 10=1+2+3+4 |
| … | … | … |
| … | N | P=1+2+3+…+（n+1） |
解决问题
班上41位同学彼此握手为礼，他们共握手多少次？小聪同学说的对不对？
问题拓展
请你用仿照上述方法来研究平面内n条直线最多有多少个交点？请你完成下表：
| 图标 | 直线条数 | 交点个数 |
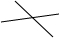 | 2 | 1 |
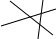 | 3 | 3=1+2 |
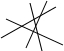 | 4 | |
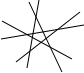 | 5 | |
| … | … | … |
| … | n |
…
7．如图所示，是一列用若干火柴棒摆成的由正三角形组成的图案：
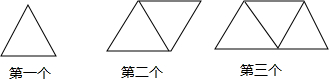
（1）完成下表的填空
（2）某同学用若干火柴棒按如上图所列的方式摆图案，摆完了第1个后，摆第2个，按着摆第3个，…，摆完第n个后剩下22根火柴棒，当他摆完第n+1个图案还多1根，问最后摆的图案是第几个图案？
（1）完成下表的填空
| 正三角形个数 | 1 | 2 | 3 | 4 | … | n |
| 火柴棒根数 | 3 | 5 | 7 | 9 | … | 2n+1 |
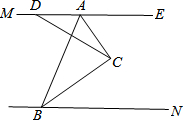如图，已知MA∥NB，CA平分∠BAE，CB平分∠ABN，点D是射线AM上一动点，连DC，当D点在射线AM（不包括A点）上滑动时，∠ADC+∠ACD+ABC的度数是否发生变化？若不变，说明理由，并求出度数．
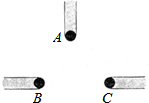（1）如图是小刚（A）、小明（B）、小勇（C）和他们各自影子的俯视图，他们所构成三角形地形的内部有一盏路灯，你认为如图是在白天阳光下的俯视图还是在晚上这盏路灯下的俯视图？